Задача 48.44 — различия между версиями
Материал из Department of Theoretical and Applied Mechanics
Sankot (обсуждение | вклад) м |
Sankot (обсуждение | вклад) (→Решение) |
||
| Строка 12: | Строка 12: | ||
==Решение== | ==Решение== | ||
| − | + | [[File:48.44.png|thumb|left|Рисунок]] | |
Уравнение Лагранжа второго рода: | Уравнение Лагранжа второго рода: | ||
| Строка 21: | Строка 21: | ||
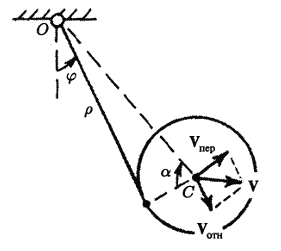
Система имеет две степени свободы: длина нити ρ и угол между нитью и вертикальной осью φ. | Система имеет две степени свободы: длина нити ρ и угол между нитью и вертикальной осью φ. | ||
| − | + | Движение цилиндра плоское, его кинетическая энергия: | |
| + | |||
| + | <math> T = \frac{1}{2}mv^{2} + \frac{1}{2}Ϳω^{2} </math> | ||
| + | |||
| + | <math>V = Vпер - Vотн </math> | ||
| + | |||
| + | <math>Vпер = dot φOC </math> | ||
| − | <math> | + | <math> OC = \sqrt{R^{2} + ρ^{2}} </math> |
| + | |||
| + | <math>T = \frac{1}{2}m(\dot φ^{2} (R^{2} + ρ^{2}) + \dot ρ^{2} - 2\dot ρ\dot φR) + \frac{1}{4}m(\frac{\dot ρ}{R} - \dot φ)^{2}</math> | ||
Потенциальная энергия: | Потенциальная энергия: | ||
| Строка 44: | Строка 52: | ||
<math>ρ^{2}\ddot φ + 2\dot φ\dot ρ ρ - Rρ\dot φ^{2} + gρsinφ = 0</math> | <math>ρ^{2}\ddot φ + 2\dot φ\dot ρ ρ - Rρ\dot φ^{2} + gρsinφ = 0</math> | ||
| − | |||
==Визуализация== | ==Визуализация== | ||
{{#widget:Iframe |url=http://tm.spbstu.ru/htmlets/Sankova_TN/48.44/111.html }} | {{#widget:Iframe |url=http://tm.spbstu.ru/htmlets/Sankova_TN/48.44/111.html }} | ||
Версия 13:44, 25 января 2018
Решение задачи 48.44 из Мещерского
Визуализация 3D-задачи по динамике на JavaScript
Исполнитель: Санькова Татьяна
Группа 23632/2 Кафедра Теоретической механики
Условие задачи
Один конец нерастяжимой тонкой нити обмотан вокруг однородного круглого цилиндра радиуса R, второй конец прикреплен к неподвижной точке O. Цилиндр, разматывая нить, опускается вниз, одновременно раскачиваясь вокруг горизонтальной оси, проходящей через точку подвеса нити. Пренебрегая массой нити, составить дифференциальные уравнения движения цилиндра.
Решение
Уравнение Лагранжа второго рода:
Система имеет две степени свободы: длина нити ρ и угол между нитью и вертикальной осью φ.
Движение цилиндра плоское, его кинетическая энергия:
Потенциальная энергия:
Находим
Визуализация