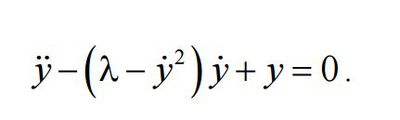Исследование уравнения Рэлея — различия между версиями
Материал из Department of Theoretical and Applied Mechanics
(→Введение) |
(→Описание задачи) |
||
| Строка 3: | Строка 3: | ||
Уравнение Рэлея(рис.1) - дифференциальное уравнение 2 порядка,которое описывает нелинейную систему с одной степенью свободы, | Уравнение Рэлея(рис.1) - дифференциальное уравнение 2 порядка,которое описывает нелинейную систему с одной степенью свободы, | ||
в которой возможны автоколебания,где λ – параметр колебательной системы.Автоколебания —незатухающие колебания, поддерживаемые внеш. источниками энергии, в нелинейной диссипативной системе | в которой возможны автоколебания,где λ – параметр колебательной системы.Автоколебания —незатухающие колебания, поддерживаемые внеш. источниками энергии, в нелинейной диссипативной системе | ||
| + | |||
| + | Задачи : | ||
| + | 1.Проанализировать уравнение с помощью метода Ван дер Поля при малых значениях параметра. | ||
| + | |||
| + | 2.Построить фазовые траектории. | ||
| + | |||
| + | 3. Понять, как влияет величина параметра на характер колебаний. | ||
== Цель : == | == Цель : == | ||
Версия 22:35, 4 июня 2017
Описание задачи
Уравнение Рэлея(рис.1) - дифференциальное уравнение 2 порядка,которое описывает нелинейную систему с одной степенью свободы, в которой возможны автоколебания,где λ – параметр колебательной системы.Автоколебания —незатухающие колебания, поддерживаемые внеш. источниками энергии, в нелинейной диссипативной системе
Задачи : 1.Проанализировать уравнение с помощью метода Ван дер Поля при малых значениях параметра.
2.Построить фазовые траектории.
3. Понять, как влияет величина параметра на характер колебаний.
Цель :
Исследование данного уравнения.
Задачи
1.Проанализировать уравнение с помощью метода Ван дер Поля при малых значениях параметра.
2.Построить фазовые траектории.
3. Понять, как влияет величина параметра на характер колебаний.