Динамическая потеря устойчивости стержня при сжатии (простейшая модель) — различия между версиями
| Строка 207: | Строка 207: | ||
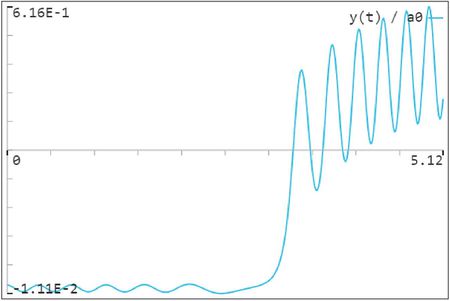
[[File:Y(t).JPG|thumb|График 1. '''<math>{\frac{\pmb Y(t)}{\pmb a_{0}}}</math>''' |слева|450px]] | [[File:Y(t).JPG|thumb|График 1. '''<math>{\frac{\pmb Y(t)}{\pmb a_{0}}}</math>''' |слева|450px]] | ||
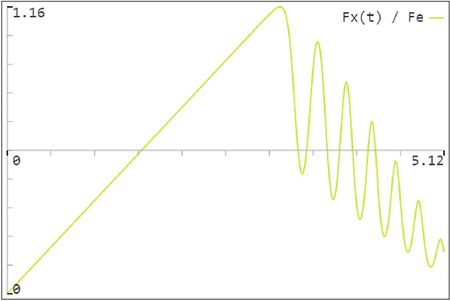
[[File:Fx(t).JPG|thumb|График 2. '''<math>{\frac{\pmb F_{x}(t)}{\pmb F_{e}}}</math>''' |справа|450px]] | [[File:Fx(t).JPG|thumb|График 2. '''<math>{\frac{\pmb F_{x}(t)}{\pmb F_{e}}}</math>''' |справа|450px]] | ||
| + | |||
| + | |||
| + | |||
Версия 16:39, 22 января 2017
Курсовые работы 2016-2017 учебного года > Динамическая потеря устойчивости стержня при сжатии (простейшая модель)Курсовой проект по Механике дискретных сред
Исполнитель: Филимонов Александр
Группа: 09 (43604/1)
Семестр: осень 2016
Формулировка задачи
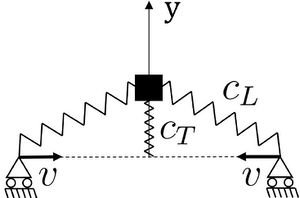
1) Смоделировать потерю устойчивости стержня как показано на Рисунке 1.
2) Построить график , где - проекция результирующей силы на ось , - Эйлерова критическая сила в статике, - время.
3) Построить график , где - координата "грузика", - равновесная длина пружинки, соответствующее половине расстояния между опорами, - время.
3) Иметь возможность менять исходные параметры: cкорость движения опор (), жесткости пружин = и = , начальное отклонение грузика от положения равновесия(), массу грузика ()
Общие сведения
Для моделирования рассмотрим простую одномерную модель, которая отражает основные физические характеристики стержня подвергающегося сжатию с постоянной скоростью. Стержень моделируется с помощью грузика, двух пружин и двух опор("стен"). Грузик связан с двумя стенками линейными пружинами с жесткостью . Поперечная жесткость стержня моделируется пружиной с жесткостью . "Стены" движутся навстречу друг другу с постоянной скоростью .
Программа
В данной программе в начальный момент времени задаются:
Скорость движения опор ().
Жесткости пружин = и = .
Начальное отклонение грузика от положения равновесия().
Масса грузика ()
Текст программы на языке JavaScript:
1 var integrator = VerletIntegrator;
2 var t = 0;
3 var dt = 0.002;
4 var step = 0;
5 var timeValue = document.getElementById('timeValue');
6 var stepFromBoard = 7;
7 var displacementData = {'x': [], 'y': []};
8 var forceData = {'x': [], 'y': []};
9 var displacementPlotCanvas = document.getElementById('displacementPlot');
10 var forcePlotCanvas = document.getElementById('forcePlot');
11 var textColor = 'rgb(51, 51, 51)';
12 var weight = undefined;
13 var springs = new Array();
14 var leftAttachment = undefined;
15 var rightAttachment = undefined;
16 var middleAttachment = createVerletElement([300, 200],null,Infinity,'isoscales triangle',[16, 10, '-y'],'Turquoise');
17 applyInitionalConditions();
18 draw();
19 function applyInitionalConditions(){
20 var displacement = +document.getElementById('displacement').value;
21 var velocity = +document.getElementById('velocity').value;
22 var stiffness1 = +document.getElementById('stiffness1').value;
23 var stiffness2 = +document.getElementById('stiffness2').value;
24 var mass = +document.getElementById('mass').value;
25 weight = createVerletElement([300, 200 - displacement],null,mass,'square',[20],'BlueViolet');
26 leftAttachment = createVerletElement([14, 200],[14 - velocity * dt, 200],Infinity,'isoscales triangle',[16, 10, '-y'],'Turquoise');
27 rightAttachment = createVerletElement([586, 200],[586 + velocity * dt, 200],Infinity,'isoscales triangle',[16, 10, '-y'],'Turquoise');
28 springs = new Array();
29 springs.push(createSpringElement(leftAttachment, weight, null, stiffness1, [12, 12], 'Tomato'));
30 springs.push(createSpringElement(rightAttachment, weight, null, stiffness1, [12, 12], 'Tomato'));
31 springs.push(createSpringElement(middleAttachment, weight, 0, stiffness2, [3, 8], 'Silver'));
32 }
33 function applyPhysics(){
34 if(t > 5.12 && keepPlaying){
35 keepPlaying = false;
36 document.getElementById('play').className = 'inactive';
37 return;
38 }
39 var deltaX, deltaY, deltalength, diff;
40 var force = {'x': 0, 'y': 0};
41 var springForceX = 0;
42 for(var i = 0; i < springs.length; ++i){
43 deltaX = springs[i].end.position.x - springs[i].start.position.x;
44 deltaY = springs[i].end.position.y - springs[i].start.position.y;
45 deltalength = Math.sqrt(Math.pow(deltaX, 2) + Math.pow(deltaY, 2));
46 if(deltalength){
47 diff = 1 - springs[i].freeLength / deltalength;
48 }else{diff = 0;}
49 force.y -= springs[i].stiffness * deltaY * diff;
50 if(0 == i){
51 springForceX = -springs[i].stiffness * deltaX * diff;
52 }
53 }
54 integrator(weight, force, dt);
55 integrator(leftAttachment, null, dt);
56 integrator(rightAttachment, null, dt);
57
58 if(!(step % 5)){
59 displacementData.x.push(t);
60 displacementData.y.push(200 - weight.position.y);
61 forceData.x.push(t);
62 forceData.y.push(springForceX);
63 plotFromData(displacementPlotCanvas, displacementData, 'y(t)', 'rgb(56, 195, 237)', undefined, textColor);
64 plotFromData(forcePlotCanvas, forceData, 'Fx(t)', 'rgb(195, 237, 56)', undefined, textColor);
65 }
66 timeValue.textContent = t.toFixed(2);
67 ++step;
68 }
69 function draw(){
70 ctx.clearRect(0, 0, canvas.width, canvas.height);
71 for(var i = 0; i < springs.length; ++i){
72 springs[i].draw();
73 }
74 leftAttachment.draw();
75 rightAttachment.draw();
76 middleAttachment.draw();
77 weight.draw();
78 }
79
80 /* Events */
81 document.getElementById('play').onclick = function(){
82 document.getElementById('conditions').className = 'hide';
83 document.getElementById('stand').className = '';
84 animate(5);
85 }
86 document.getElementById('displacement').onchange = function(){
87 document.getElementById('displacementValue').textContent = (+this.value).toFixed(1);
88 applyInitionalConditions();
89 draw();
90 }
91 document.getElementById('velocity').onchange = function(){
92 document.getElementById('velocityValue').textContent = (+this.value).toFixed(1);
93 applyInitionalConditions();
94 draw();
95 }
96 document.getElementById('stiffness1').onchange = function(){
97 document.getElementById('stiffness1Value').textContent = (+this.value).toFixed(1);
98 applyInitionalConditions();
99 draw();
100 }
101 document.getElementById('stiffness2').onchange = function(){
102 document.getElementById('stiffness2Value').textContent = (+this.value).toFixed(1);
103 applyInitionalConditions();
104 draw();
105 }
106 document.getElementById('mass').onchange = function(){
107 document.getElementById('massValue').textContent = (+this.value).toFixed(1);
108 applyInitionalConditions();
109 draw();
110 }
111 function drawSpringElement(){
112 drawSpring(
113 this.start.position.x,
114 this.end.position.x,
115 this.start.position.y,
116 this.end.position.y,
117 this.sizes[0],
118 this.sizes[1],
119 this.color
120 );
121 }
122 function drawSpring(xStart, xEnd, yStart, yEnd, n, h, color){
123 ctx.beginPath();
124 ctx.lineWidth = 2;
125 ctx.strokeStyle = color;
126 var L = xEnd - xStart;
127 var Ly = yEnd - yStart;
128 for (var i = 0; i < n; ++i){
129 var x_st = xStart + L / n * i;
130 var y_st = yStart + Ly / n * i;
131 var x_end = xStart + L / n * (i + 1);
132 var y_end = yStart + Ly / n * (i + 1);
133 var l = x_end - x_st;
134 var ly = y_end - y_st;
135 ctx.beginPath();
136 ctx.bezierCurveTo(x_st, y_st, x_st + l / 4, y_st + ly / 4 + h, x_st + l / 2, y_st + ly / 2);
137 ctx.bezierCurveTo(x_st + l / 2, y_st + ly / 2, x_st + 3 * l / 4, y_st + 3 * ly / 4 - h, x_st + l, y_st + ly);
138 ctx.stroke();
139 }
140 ctx.closePath();
141 }
Результаты
Здесь приведены конечные результаты, при заданных начальных параметрах.
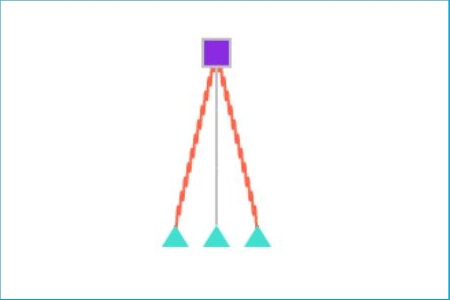
На Рисунке 2 предоставлено конечное положение грузика, при заданном времени.
На Графике 1 мы наблюдаем, что на некотором расстоянии между стенками (через некоторое время после начала движения стен) равновесие становится неустойчивым.
На Графике 2 мы видим проекцию результируещей силы во времени на ось
Ссылки
- Vitaly A. Kuzkin Structural model for the dynamic buckling of a column under constant rate compression