Траектория движения частицы в однородном магнитном поле — различия между версиями

Версия 21:43, 21 декабря 2016

Содержательная постановка

Модель должна позволять:

• Вычислять положение частицы в любой момент времени;
• Изучать природу движения частицы в магнитном поле при различных начальных параметрах.

Входные данные:

• Масса и радиус частицы;
• Начальная скорость;
• Начальные координаты;
• Коэффициент плотности среды;
• Промежуток времени, в течение которого происходит движение частицы.

Концептуальная постановка

• Объектом моделирования является частица радиуса R и заряда q;
• Будем считать частицу материальной точкой массой m, положение которой совпадает с центром масс частицы;
• Движение происходит в однородном магнитном поле под действием силы Лоренца;
• Движение происходит в трехмерном пространстве (оси Ox, Oy, Oz);
• Пренебрегаем возмущениями, вызванными собственным вращением частицы, но учитываем коэффициент плотности среды.

Математическая постановка

• Сила Лоренца [math]F = q*v*b[/math]
• Сила сопротивления среды [math]r0*v[/math]
• Ускорение [math]a = F/m — r0*v/m[/math] (по 2 закону Ньютона)

• В проекциях на оси координат

[math] ax = q/m*(bz*vy-by*vz)-vx*ro/m; ay = q/m*(bx*vz-bz*vx)-vy*ro/m; az = q/m*(by*vx-bx*vy)-vz*ro/m; [/math]

• Скорость [math]v=v0 +a*t[/math]

• В проекциях на оси координат

[math] vx+=ax*dt; vy+=ay*dt; vz+=az*dt; [/math]

• Координата вычисляется с учетом того, что в короткие временные промежутки dt движение частицы считается равноускоренным

[math] x = x0 + v0*t - a*t^2/2 [/math]

• В проекциях на оси координат

[math] x = x0+vx*dt+ax*dt*dt/2; y = y0+vy*dt+ay*dt*dt/2; z = z0+vz*dt+az*dt*dt/2; [/math]

Проверка адекватности

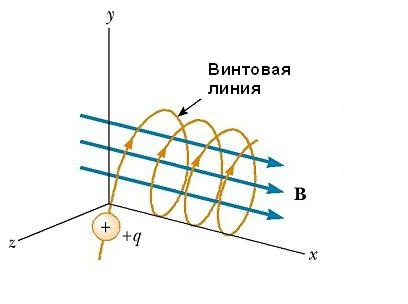
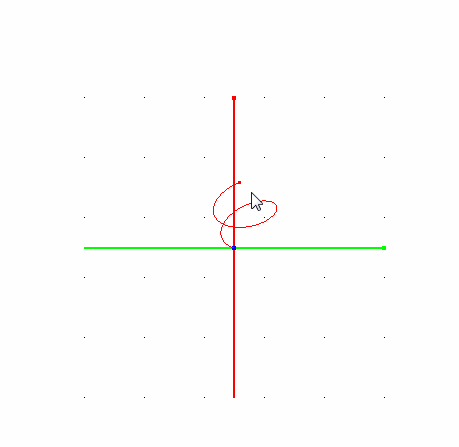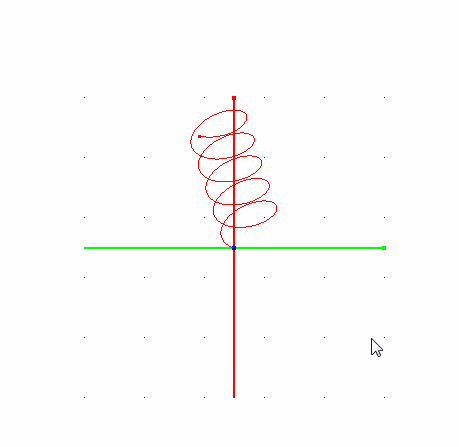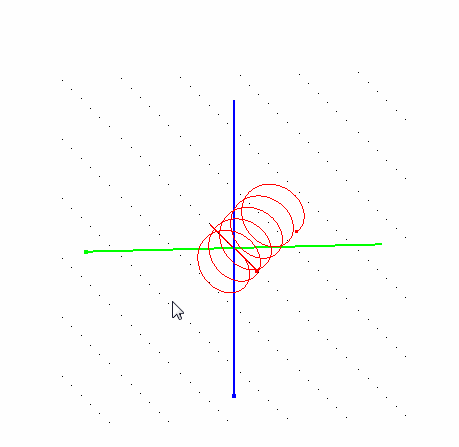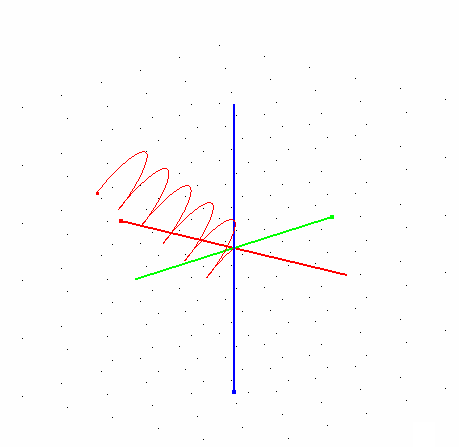
• Траектория частицы в однородном магнитном поле должна быть винтовой линией.
• Радиус спирали с течением времени должен уменьшаться вследствие взаимодействия со средой

Пример результата

Презентация

• File:proekt0.pptx

Авторы

• Тур Всеволод
• Серов Александр
• Носов Александр
• Букреев Павел