Обратный каскад энергии(двумерная турбулентность) — различия между версиями
(→top) |
(→top) |
||
| Строка 27: | Строка 27: | ||
где <big><math>\pmb r_{ij} =\pmb r_{i} - \pmb r_{j},\; \pmb e_{ij} = \frac{\pmb r_{ij}}{r_{ij}},\; a_{c}</math></big> - радиус обрезания, <big><math>a, D</math></big> - энергетические параметры системы, <big><math> \beta </math></big> - коэффициент вязкости. | где <big><math>\pmb r_{ij} =\pmb r_{i} - \pmb r_{j},\; \pmb e_{ij} = \frac{\pmb r_{ij}}{r_{ij}},\; a_{c}</math></big> - радиус обрезания, <big><math>a, D</math></big> - энергетические параметры системы, <big><math> \beta </math></big> - коэффициент вязкости. | ||
| + | |||
| + | Диссипативные силы уменьшают полную энергию системы. Таким образом, без внешнего добавления энергии система перейдет в состояние равновесия. В данной модели энергия добавляется при помощи термостата Берендсена. Скорости частиц на каждом шаге по времени перемножаются на параметр <big><math> s </math></big> : | ||
| + | |||
| + | <big><math> s = \sqrt{\frac{T_{0}}{T}},\qquad T =\frac{1}{2}\sum_{i} m {\pmb v_{i}}^{2} </math></big> | ||
| + | |||
| + | где <big><math> T </math></big> - температура среды | ||
==Программа== | ==Программа== | ||
==Анализ== | ==Анализ== | ||
==Ссылки== | ==Ссылки== | ||
Версия 23:44, 15 декабря 2016
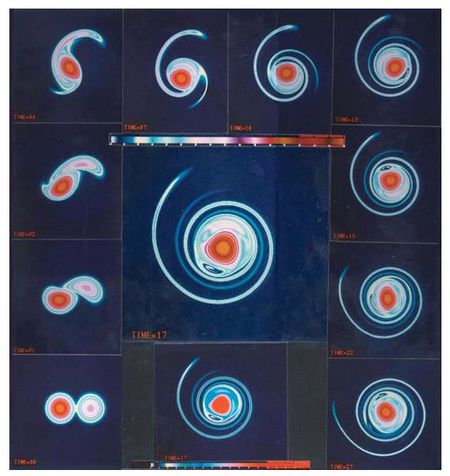
Переход энергии с микро на макро уровень (и обратно) - одно из фундаментальных физических явлений. В данной работе,на примере двумерных турбулентных вихрей, рассматривается случай перехода с мелкомасштабного механического движения на крупномасштабное. В литературе это явление обычно упоминается как “обратный каскад” энергии. Построенная модель позволяет исследовать переход энергии с микро на макро уровень и корреляции скоростей в дискретной среде.
Модель представлена набором взаимодействующих частиц с случайными начальными скоростями. Частицы взаимодействуют за счет отталкивающих потенциальных и диссипативных сил. Динамика взаимодействия описана набором уравнений движения Ньютона:
где m, r - масса и радиус вектор i-ой частицы, - отталкивающая потенциальная и диссипативная силы соответственно.
Выражения для потенциальной и диссипативной сил:
где - радиус обрезания, - энергетические параметры системы, - коэффициент вязкости.
Диссипативные силы уменьшают полную энергию системы. Таким образом, без внешнего добавления энергии система перейдет в состояние равновесия. В данной модели энергия добавляется при помощи термостата Берендсена. Скорости частиц на каждом шаге по времени перемножаются на параметр :
где - температура среды