Колебания материальной точки в поле силы тяжести — различия между версиями
Материал из Department of Theoretical and Applied Mechanics
(содержание6) |
(бла) |
||
| Строка 3: | Строка 3: | ||
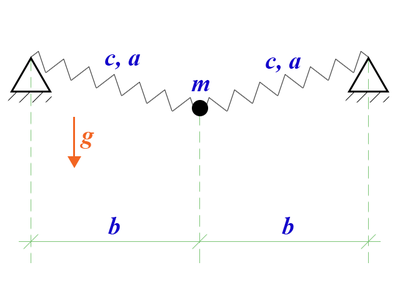
Рассмотрим механическую систему с двумя степенями свободы: материальная точка массы <math>m</math> связана пружинами с двумя опорами, вся система находится в поле силы тяжести. Расстояние между опорами <math>2b</math>, длина пружин в недеформированном состоянии <math>a</math>, жесткость пружин <math>c</math>. | Рассмотрим механическую систему с двумя степенями свободы: материальная точка массы <math>m</math> связана пружинами с двумя опорами, вся система находится в поле силы тяжести. Расстояние между опорами <math>2b</math>, длина пружин в недеформированном состоянии <math>a</math>, жесткость пружин <math>c</math>. | ||
[[File:Scheme l.png|400px|left|Схема]] | [[File:Scheme l.png|400px|left|Схема]] | ||
| + | Уравнения движения системы будут выглядеть так: | ||
| + | ::<math> | ||
| + | \left\{ | ||
| + | \begin{array}{ll} | ||
| + | m \ddot{x} = -c_{2}x_{1}+c_{2}x_{2}-c_{2}l_{20}-c_{1}x_{1}+c_{1}l_{10} \\ | ||
| + | \displaystyle m \ddot{y} = -c_{2}x_{2}+c_{2}x_{1}+c_{2}l_{20} \\ | ||
| + | \end{array} | ||
| + | \right. | ||
| + | </math> | ||
Версия 13:56, 6 октября 2016
Виртуальная лаборатория > Колебания материальной точки в поле силы тяжестиКраткое описание системы
Рассмотрим механическую систему с двумя степенями свободы: материальная точка массы связана пружинами с двумя опорами, вся система находится в поле силы тяжести. Расстояние между опорами , длина пружин в недеформированном состоянии , жесткость пружин .
Уравнения движения системы будут выглядеть так: