Ауксетики — различия между версиями
| Строка 7: | Строка 7: | ||
Ученым известны материалы с подобными свойствами уже около 100 лет, но в настоящее время им уделяют повышенное внимание. Один из первых синтетических ауксетиков был описан в 1987 году в статье под названием «Foam structures with a Negative Poisson’s Ratio» («Пенные структуры с отрицательным коэффициентом Пуассона») [2]. | Ученым известны материалы с подобными свойствами уже около 100 лет, но в настоящее время им уделяют повышенное внимание. Один из первых синтетических ауксетиков был описан в 1987 году в статье под названием «Foam structures with a Negative Poisson’s Ratio» («Пенные структуры с отрицательным коэффициентом Пуассона») [2]. | ||
| − | + | Композиты с отрицательным коэффициентом Пуассона был предсказаны еще в 1985 году [3-4]. | |
| − | В работах научной группы под руководством Р.В. Гольдштейна [ | + | В работах научной группы под руководством Р.В. Гольдштейна [5-7] разработаны основы ауксетической механики кристаллических материалов. В работе [8] получена связь упругих свойств ряда ауксетиков с характеристиками их микроструктуры. |
| − | + | На стенде внизу приведен пример ауксетика с одной степенью свободы. За обобщенную координату выбран угол поворота квадрата. Для его изменения можно воспользоваться слайдером или потянуть мышкой за правую стенку. Также можно пронаблюдать колебания в подобной системе. Частота колебаний задается соответствующим слайдером. | |
{{#widget:Iframe |url=http://tm.spbstu.ru/htmlets/Sokolov/auxetic.html |width=900 |height=650 |border=0 }} | {{#widget:Iframe |url=http://tm.spbstu.ru/htmlets/Sokolov/auxetic.html |width=900 |height=650 |border=0 }} | ||
| Строка 20: | Строка 20: | ||
# Evans K.E. Auxetic polymers: a new range of materials. Endeavour. New series. 1991. V. 15. № 4. P. 170–174. | # Evans K.E. Auxetic polymers: a new range of materials. Endeavour. New series. 1991. V. 15. № 4. P. 170–174. | ||
| − | |||
# Lakes R.S. Foam structures with a negative Poisson’s ratio. Science. 1987. V. 235. № 4792. P. 1038–1040. | # Lakes R.S. Foam structures with a negative Poisson’s ratio. Science. 1987. V. 235. № 4792. P. 1038–1040. | ||
| − | + | # Колпаков А.Г. К определению усредненных характеристик упругих каркасов. Прикладная математика и механика, 6, 1985, pp.969-977. | |
| + | # Almgren R.F. An isotropic three-dimensional structure with Poisson's ratio=-1, J. Elasticity 15 (1985), 427-430. | ||
# Гольдштейн Р.В., Городцов В.А., Лисовенко Д.С. Ауксетическая механика кристаллических материалов. Известия Российской академии наук. Механика твердого тела. 2010. № 4. С. 43-62. | # Гольдштейн Р.В., Городцов В.А., Лисовенко Д.С. Ауксетическая механика кристаллических материалов. Известия Российской академии наук. Механика твердого тела. 2010. № 4. С. 43-62. | ||
| − | |||
# Гольдштейн Р.В., Городцов В.А., Лисовенко Д.С. Модули юнга и коэффициенты пуассона криволинейно анизотропных гексагональных и ромбоэдрических нанотрубок. Нанотрубки-ауксетики. Доклады Академии наук. 2013. Т. 452. № 3. С. 279. | # Гольдштейн Р.В., Городцов В.А., Лисовенко Д.С. Модули юнга и коэффициенты пуассона криволинейно анизотропных гексагональных и ромбоэдрических нанотрубок. Нанотрубки-ауксетики. Доклады Академии наук. 2013. Т. 452. № 3. С. 279. | ||
| − | |||
# Гольдштейн Р.В., Городцов В.А., Лисовенко Д.С. Изменчивость коэффициента Пуассона для гексагональных кристаллов под давлением. Труды МАИ. 2016. № 87. С. 1. | # Гольдштейн Р.В., Городцов В.А., Лисовенко Д.С. Изменчивость коэффициента Пуассона для гексагональных кристаллов под давлением. Труды МАИ. 2016. № 87. С. 1. | ||
| − | |||
# Berinskii I.E. Elastic networks to model auxetic properties of cellular materials. International Journal of Mechanical Sciences 115-116 (2016) 481–488. | # Berinskii I.E. Elastic networks to model auxetic properties of cellular materials. International Journal of Mechanical Sciences 115-116 (2016) 481–488. | ||
Версия 14:12, 10 сентября 2016
Виртуальная лаборатория > АуксетикиАуксетики (от греч. αὐξητικός) — материалы, имеющие отрицательные значения коэффициента Пуассона. Термин введен профессором Кеном Эвансом (Ken Evans) из Эксетерского университета [1].
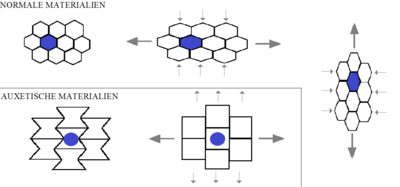
При растяжении материалы-ауксетики становятся толще в направлении, перпендикулярном приложенной силе. Это происходит из-за шарнирно-подобной структуры ауксетиков, которая деформируется при растяжении. Такое свойство может обусловливаться свойствами отдельных молекул или определяться структурными особенностями материала на макроскопическом уровне. От материалов этого типа ожидаются хорошие механические свойства, такие как значительное поглощение механической энергии и высокое сопротивление разрушению.
Ученым известны материалы с подобными свойствами уже около 100 лет, но в настоящее время им уделяют повышенное внимание. Один из первых синтетических ауксетиков был описан в 1987 году в статье под названием «Foam structures with a Negative Poisson’s Ratio» («Пенные структуры с отрицательным коэффициентом Пуассона») [2]. Композиты с отрицательным коэффициентом Пуассона был предсказаны еще в 1985 году [3-4].
В работах научной группы под руководством Р.В. Гольдштейна [5-7] разработаны основы ауксетической механики кристаллических материалов. В работе [8] получена связь упругих свойств ряда ауксетиков с характеристиками их микроструктуры.
На стенде внизу приведен пример ауксетика с одной степенью свободы. За обобщенную координату выбран угол поворота квадрата. Для его изменения можно воспользоваться слайдером или потянуть мышкой за правую стенку. Также можно пронаблюдать колебания в подобной системе. Частота колебаний задается соответствующим слайдером.
Автор: Алексей Соколов
Литература
- Evans K.E. Auxetic polymers: a new range of materials. Endeavour. New series. 1991. V. 15. № 4. P. 170–174.
- Lakes R.S. Foam structures with a negative Poisson’s ratio. Science. 1987. V. 235. № 4792. P. 1038–1040.
- Колпаков А.Г. К определению усредненных характеристик упругих каркасов. Прикладная математика и механика, 6, 1985, pp.969-977.
- Almgren R.F. An isotropic three-dimensional structure with Poisson's ratio=-1, J. Elasticity 15 (1985), 427-430.
- Гольдштейн Р.В., Городцов В.А., Лисовенко Д.С. Ауксетическая механика кристаллических материалов. Известия Российской академии наук. Механика твердого тела. 2010. № 4. С. 43-62.
- Гольдштейн Р.В., Городцов В.А., Лисовенко Д.С. Модули юнга и коэффициенты пуассона криволинейно анизотропных гексагональных и ромбоэдрических нанотрубок. Нанотрубки-ауксетики. Доклады Академии наук. 2013. Т. 452. № 3. С. 279.
- Гольдштейн Р.В., Городцов В.А., Лисовенко Д.С. Изменчивость коэффициента Пуассона для гексагональных кристаллов под давлением. Труды МАИ. 2016. № 87. С. 1.
- Berinskii I.E. Elastic networks to model auxetic properties of cellular materials. International Journal of Mechanical Sciences 115-116 (2016) 481–488.