КП: Параметрические колебания — различия между версиями
Sizovaea (обсуждение | вклад) |
Sizovaea (обсуждение | вклад) |
||
| Строка 46: | Строка 46: | ||
Примечание: менять частоту колебаний лучше в центральном положении. | Примечание: менять частоту колебаний лучше в центральном положении. | ||
| − | {{#widget:Iframe |url=http://tm.spbstu.ru/htmlets/ | + | {{#widget:Iframe |url=http://tm.spbstu.ru/htmlets/Sizova/dl_example_Swing.html |width=830 |height=630 |border=0 }} |
<div class="mw-collapsible mw-collapsed"> | <div class="mw-collapsible mw-collapsed"> | ||
'''Текст программы на языке JavaScript:''' <div class="mw-collapsible-content"> | '''Текст программы на языке JavaScript:''' <div class="mw-collapsible-content"> | ||
Версия 16:48, 25 июня 2016
Курсовой проект по Теории колебаний
Исполнитель: Сизова Екатерина
Группа: 09 (33604)
Семестр: весна 2016
Содержание
Аннотация проекта
Колебания — это повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия. По характеру взаимодействия с окружающей средой колебания делятся на вынужденные, свободные, автоколебания, случайные и параметрические, которым и посвящена данная работа.
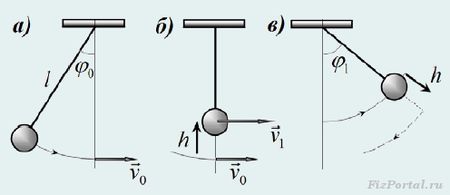
Параметрические колебания - колебания, возникающие при изменении какого-либо параметра колебательной системы в результате внешнего воздействия. Одним из классических примеров параметрических колебаний является система, состоящая из качелей и человека, раскачивающего их.
Формулировка задачи
Описать математически движение качелей и смоделировать их движение.
Решение
Существует два способа раскачивания качелей: качели может раскачивать человек, находящийся вне качелей, а также человек, который сидит или стоит на них. В данной задаче будет рассматриваться второй случай - человек, стоящий на качелях, периодически, в нужные моменты приседает и встает. При этом периодически изменяются параметры самой колебательной системы, поэтому такие колебания можно назвать параметрическими. Простейшим уравнением, описывающим такие колебания, является уравнение гармонических колебаний, где . является периодической функцией времени .
Зависимость параметра от времени может быть, например, представлена в виде , где постоянная - собственная частота колебаний при неизменных средних значениях параметров системы(например, частота свободных колебаний качелей при неподвижно стоящем на них человеке), а второе слагаемое описывает периодическое изменение параметров системы.
Будем считать человека материальной точкой, расстояние от которой до оси вращения может изменяться в некоторых небольших пределах "сознательно", то есть в нужные моменты времени. Для того, чтобы максимально увеличить механическую энергию колебаний, человек должен вставать, когда для этого требуется приложить максимальное усилие, так как при этом будет совершена максимальная работа. Очевидно, это условие достигается, когда качели проходят нижнюю точку.
Итак, пусть начальный угол отклонения качелей равен и при этом максимальном отклонении центр масс находится на максимальной удалении от точки подвеса .
Когда качели опустятся под действием силы тяжести в нижнее положение, рассматриваемая материальная точка приобретет скорость , которую можно найти на основании закона сохранения энергии , из которого следует .
Далее пусть в момент прохождения нижней точки центр масс очень быстро поднимается на малую высоту , при этом его скорость возрастает до некоторой величины . На основании закона сохранения импульса . Из этого уравнения находим , учитывая, что высота подъема значительно меньше длины качелей .
Теперь с помощью закона сохранения энергии можно найти максимальный угол отклонения качелей в противоположном направлении, который удовлетворяет условию .
Оценим изменение высоты подъема за этот же промежуток времени
.
Визуализация задачи
Примечание: менять частоту колебаний лучше в центральном положении.
Файл "dl_example_Swing.js"
1 function main_dl_example_Swing() {
2
3 number_input.oninput = function() {
4 slider_input.value = number_input.value;
5 mult2();
6 };
7 slider_input.oninput = function() {
8 number_input.value = slider_input.value;
9 mult2();
10 };
11
12 function mult2() {
13 span_result.innerHTML = Math.PI / number_input.value;
14 }
15
16 var ctx = canvas_Swing.getContext("2d");
17 var width = canvas_Swing.width;
18 var height = canvas_Swing.height;
19
20 var string_s_x = 400;
21 var string_s_y = 10;
22 var string_e_x = 400;
23 var string_e_y = 300;
24 var phi = Math.PI / 2;
25 //var n = 6;
26 var phi_max = Math.PI / number_input.value;
27 var h = 20;
28 var m = 10;
29 var string_length = 290;
30 var direction = 1;
31 var speed = 1;
32
33 var board_s_x = string_s_x - 50;
34 var board_s_y = string_e_y;
35 var board_e_x = string_e_x + 50;
36 var board_e_y = string_e_y;
37
38 var head_x = string_e_x + 15;
39 var head_y = string_e_y - 50;
40 var head_r = 10;
41
42 var eye_left_x = head_x - 2;
43 var eye_left_y = head_y - 2;
44 var eye_right_x = head_x + 2;
45 var eye_right_y = head_y - 2;
46
47 var body_s_x = head_x + 4;
48 var body_s_y = head_y + head_r;
49 var body_e_x = body_s_x + 12;
50 var body_e_y = body_s_y + 25;
51
52 var legs_s_x = body_e_x;
53 var legs_s_y = body_e_y;
54 var legs_e_x = body_e_x - 20;
55 var legs_e_y = board_e_y + 10;
56
57 var arms_s_x = body_e_x - 5;
58 var arms_s_y = body_e_y - 8;
59 var arms_e_x = body_e_x - 25;
60 var arms_e_y = body_e_y - 15;
61
62 function step() {
63 tick();
64 draw();
65 }
66
67 function tick() {
68 phi_max = Math.PI / number_input.value;
69
70 string_e_x = string_s_x + string_length * Math.cos(phi);
71 string_e_y = string_s_y + string_length * Math.sin(phi);
72
73 speed = 0.017 * Math.sqrt((Math.cos(phi - Math.PI / 2) - Math.cos(phi_max + 0.01)));
74 phi = phi + direction * speed;
75
76 if (phi > Math.PI / 2 + phi_max) direction = - direction;
77 if (phi < Math.PI / 2 - phi_max) direction = - direction;
78
79 board_s_x = string_s_x - 50;
80 board_s_y = string_e_y;
81 board_e_x = string_e_x + 50;
82 board_e_y = string_e_y;
83
84 head_x = string_e_x + 15;
85 head_y = string_e_y - 50;
86 head_r = 10;
87
88 eye_left_x = head_x - 2;
89 eye_left_y = head_y - 2;
90 eye_right_x = head_x + 2;
91 eye_right_y = head_y - 2;
92
93 body_s_x = head_x + 4;
94 body_s_y = head_y + head_r;
95 body_e_x = body_s_x + 12;
96 body_e_y = body_s_y + 25;
97
98 legs_s_x = body_e_x;
99 legs_s_y = body_e_y;
100 legs_e_x = body_e_x - 20;
101 legs_e_y = board_e_y + 10;
102
103 arms_s_x = body_e_x - 5;
104 arms_s_y = body_e_y - 8;
105 arms_e_x = body_e_x - 25;
106 arms_e_y = body_e_y - 15;
107
108 }
109
110 function draw() {
111 ctx.clearRect(0, 0, width, height);
112 ctx.beginPath();
113
114 ctx.lineWidth="1";
115 ctx.strokeStyle="#080101";
116
117 ctx.moveTo(string_s_x, string_s_y);
118 ctx.lineTo(string_e_x, string_e_y);
119 ctx.stroke();
120
121 ctx.lineWidth="2";
122 ctx.strokeStyle="#DED5D5";
123 ctx.beginPath();
124 ctx.arc(head_x, head_y, head_r, 0, 2 * Math.PI);
125 ctx.stroke();
126
127 ctx.fillStyle="#080101";
128 ctx.beginPath();
129 ctx.arc(eye_left_x, eye_left_y, 1, 0, 2 * Math.PI);
130 ctx.arc(eye_right_x, eye_right_y, 1, 0, 2 * Math.PI);
131 ctx.fill();
132
133 ctx.beginPath();
134 ctx.strokeStyle="#DED5D5";
135 ctx.moveTo(body_s_x, body_s_y);
136 ctx.lineTo(body_e_x, body_e_y);
137 ctx.lineWidth="6";
138 ctx.stroke();
139
140 ctx.beginPath();
141 ctx.strokeStyle="#DED5D5";
142 ctx.moveTo(legs_s_x, legs_s_y);
143 ctx.lineTo(legs_e_x, legs_e_y);
144 ctx.lineWidth="6";
145 ctx.stroke();
146
147 ctx.beginPath();
148 ctx.strokeStyle="#DED5D5";
149 ctx.moveTo(arms_s_x, arms_s_y);
150 ctx.lineTo(arms_e_x, arms_e_y);
151 ctx.lineWidth="6";
152 ctx.stroke();
153
154 ctx.fillStyle="#F31C1C";
155 ctx.beginPath();
156 ctx.arc(string_e_x, string_e_y, head_r, 0, 2 * Math.PI);
157 ctx.fill();
158
159 ctx.lineWidth="2";
160 ctx.strokeStyle="#080101";
161 ctx.beginPath();
162 ctx.arc(string_e_x, string_e_y, head_r, 0, 2 * Math.PI);
163 ctx.stroke();
164 }
165
166 setInterval(step, 1000 / 60);
167
168 }
Файл "dl_example_Swing.html" <syntaxhighlight lang="javascript" line start="1" enclose="div"> <!DOCTYPE html> <html> <head>
<title>SWING</title> <script src="dl_example_Swing.js">
function sizePic() { number_input = document.getElementById("number_input").value;
} </script> </head> <body onload="main_dl_example_Swing();">
<canvas id="canvas_Swing" width="800" height="450" style="border: 1px solid #000000"></canvas>
<input type="range" id="slider_input" min=3 max=9 value=3 step=0.01 style="width: 150px;">
</body> </html>