Вязкоупругая модель склеральной оболочки глаза — различия между версиями
(→Постановка задачи) |
(→Введение) |
||
| Строка 3: | Строка 3: | ||
''Научный руководитель'': [[Е.Н.Вильчевская | к.ф-м.н., доцент Е.Н. Вильчевская]]<br> | ''Научный руководитель'': [[Е.Н.Вильчевская | к.ф-м.н., доцент Е.Н. Вильчевская]]<br> | ||
| − | ==Введение== | + | ==Введение и мотивация работы== |
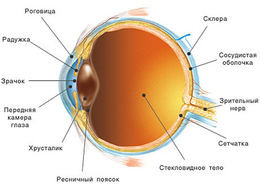
[[Файл:Secheniye_glaza.png|260px|thumb|right|]] | [[Файл:Secheniye_glaza.png|260px|thumb|right|]] | ||
При построении простейших моделей глаза можно считать, что он имеет шаровидную форму. Глаз заполнен прозрачной гелеобразной субстанцией, называемой стекловидным телом. Во внешней фиброзной оболочке глаза можно выделить наружную фиброзную, среднюю сосудистую и внутреннюю сетчатую оболочки. Наружная фиброзная (корнеосклеральная) оболочка глаза выполняет защитную функцию и обуславливает форму глаза. Она состоит из передней прозрачной части - роговицы, - и задней непрозрачной части – склеры, обладающих различными радиусами кривизны и биомеханическими характеристиками. Склера занимает 93% внешней фиброзной оболочки глаза человека, поэтому в задачах, связанных с определением формы и изменением объема глазного яблока под действием внутриглазного давления (ВГД), биомеханические свойства склеры играют решающую роль, и поведение глаза допустимо моделировать поведением его склеральной оболочки. | При построении простейших моделей глаза можно считать, что он имеет шаровидную форму. Глаз заполнен прозрачной гелеобразной субстанцией, называемой стекловидным телом. Во внешней фиброзной оболочке глаза можно выделить наружную фиброзную, среднюю сосудистую и внутреннюю сетчатую оболочки. Наружная фиброзная (корнеосклеральная) оболочка глаза выполняет защитную функцию и обуславливает форму глаза. Она состоит из передней прозрачной части - роговицы, - и задней непрозрачной части – склеры, обладающих различными радиусами кривизны и биомеханическими характеристиками. Склера занимает 93% внешней фиброзной оболочки глаза человека, поэтому в задачах, связанных с определением формы и изменением объема глазного яблока под действием внутриглазного давления (ВГД), биомеханические свойства склеры играют решающую роль, и поведение глаза допустимо моделировать поведением его склеральной оболочки. | ||
Версия 18:29, 16 июня 2016
МАГИСТЕРСКАЯ РАБОТА
Автор работы: К.П. Фролова
Научный руководитель: к.ф-м.н., доцент Е.Н. Вильчевская
Введение и мотивация работы
При построении простейших моделей глаза можно считать, что он имеет шаровидную форму. Глаз заполнен прозрачной гелеобразной субстанцией, называемой стекловидным телом. Во внешней фиброзной оболочке глаза можно выделить наружную фиброзную, среднюю сосудистую и внутреннюю сетчатую оболочки. Наружная фиброзная (корнеосклеральная) оболочка глаза выполняет защитную функцию и обуславливает форму глаза. Она состоит из передней прозрачной части - роговицы, - и задней непрозрачной части – склеры, обладающих различными радиусами кривизны и биомеханическими характеристиками. Склера занимает 93% внешней фиброзной оболочки глаза человека, поэтому в задачах, связанных с определением формы и изменением объема глазного яблока под действием внутриглазного давления (ВГД), биомеханические свойства склеры играют решающую роль, и поведение глаза допустимо моделировать поведением его склеральной оболочки.
На экспериментальных кривых, соответствующих изменению ВГД в течение нескольких минут после введения интравитреальной инъекции - инъекции внутрь стекловидного тела, - наблюдается его резкий скачок непосредственно после инъекции, вызванный увеличением объема, а затем спад до некоторого постоянного значения. В большинстве существующих источников литературы данный спад объясняется наличием оттока внутриглазной жидкости из нагруженного глаза. В связи с уменьшением объема происходит уменьшение ВГД. Однако известно, что склере присуща вязкоупругая реакция на приложенную нагрузку. Непосредственное измерение вязкости склеры вызывает технические сложности и, в связи с этим, в литературе отсутствуют сведения о соответствующих параметрах вязкости. Это приводит к тому, что в большинстве существующих моделей вязкие свойства склеры игнорируются, а поведение склеры при нагрузках предполагается чисто упругим. В данной работе релаксация напряжений (спад ВГД) в глазу после введения интравитреальной инъекции объясняется не только наличием оттока внутриглазной жидкости из нагруженного глаза, но и вязкими свойствами склеральной оболочки глаза. В рамках данной работы будет предложен метод определения коэффициента сдвиговой вязкости склеры, заключающийся сравнении результатов математического моделирования и указанных в литературе экспериментальных данных, основанных на дискретном измерении ВГД в течение нескольких минут после интравитреальной инъекции. Будут рассмотрены различные варианты постановки граничных условий. В первом случае будет предполагаться, что введенный при инъекции дополнительный объем жидкости сохраняется в стекловидном теле на протяжении времени проведения эксперимента, релаксация напряжений будет объясняться только наличием вязких свойств склеры. Во втором случае будет учитываться отток внутриглазной жидкости, релаксация напряжений будет объясняться наличием обоих факторов: и наличием вязких свойств склеры, и наличием оттока внутриглазной жидкости из нагруженного глаза. Будет определяться значение коэффициента сдвиговой вязкости, при котором отклонение теоретических данных от экспериментальных минимально.
Цели исследования
- Смоделировать вязкоупругое поведение склеры после интравитреальной инъекции — инъекции внутрь стекловидного тела;
- Определить значение коэффициента сдвиговой вязкости склеры путем сравнения результатов математического моделирования и указанных в литературе экспериментальных данных, основанных на дискретном измерении внутриглазного давления (ВГД) в течение нескольких минут после интравитреальной инъекции.
Постановка задачи
Моделируемый в рамках данной работы эксперимент основан на дискретном измерении ВГД в течение нескольких минут после введения интравитреальной инъекции в объеме 0,05 мл. Точки на экспериментальной кривой соответствуют средним значениям ВГД для 34 пациентов. Для контроля состояния пациентов ВГД измерялось также и на парном не вакцинированном глазу. Задача моделируется вязкоупругим сферическим слоем с внутренним радиусом и внешним радиусом при центральносимметричной нагрузке: внешнее давление отсутствует, на внутреннем радиусе заданы перемещения, учитывающие величину дополнительного объема жидкости, введенного при инъекции. Задание нулевого давления на внешнем радиусе объясняется тем, что по определению ВГД есть разница между атмосферным давлением и давлением в глазу. Материал склеры предполагается линейным трансверсально – изотропным. Задача решается в рамках трехмерной теории линейной вязкоупругости.