Случайная упаковка шаров — различия между версиями
| Строка 3: | Строка 3: | ||
== Краткое описание == | == Краткое описание == | ||
| − | Рассматривается задача плотной упаковки шаров заданного радиуса в квадрате и круге. Так же в ходе исследования выявляется наиболее плотная 2D упаковка из рассматриваемых. | + | Рассматривается задача плотной упаковки шаров заданного радиуса в квадрате и круге. Так же в ходе исследования выявляется наиболее плотная 2D упаковка из рассматриваемых. |
| + | |||
Программа генерирует последовательно круги разного радиуса в заданной области(квадрат или круг) до тех пор, пока <math> k </math> раз подряд не получим неудачный эксперимент, т.е. наш круг будет выходить за заданную область или задевать другие круги. | Программа генерирует последовательно круги разного радиуса в заданной области(квадрат или круг) до тех пор, пока <math> k </math> раз подряд не получим неудачный эксперимент, т.е. наш круг будет выходить за заданную область или задевать другие круги. | ||
Версия 13:31, 6 мая 2016
Виртуальная лаборатория > Случайная упаковка шаров
Краткое описание
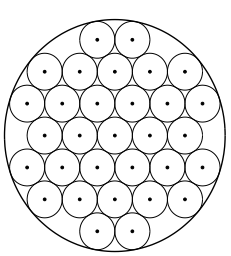
Рассматривается задача плотной упаковки шаров заданного радиуса в квадрате и круге. Так же в ходе исследования выявляется наиболее плотная 2D упаковка из рассматриваемых.
Программа генерирует последовательно круги разного радиуса в заданной области(квадрат или круг) до тех пор, пока раз подряд не получим неудачный эксперимент, т.е. наш круг будет выходить за заданную область или задевать другие круги.
Для запуска программы выберите, какой эксперимент хотите провести - случайная упаковка в квадрате ( кнопка "square") или в круге (кнопка "circle") и нажмите "старт". Так же мы можем варьировать отношение диаметра маленького кружка к стороне квадрата/диаметру большого круга и количество экспериментов - и кол-во "неудачных" экспериментов .
После наших экспериментов мы построили график зависимости удельного числа проводимых экспериментов(т.е. отношение кол-ва экспериментов с данной плотностью к общему числу экспериментов) от плотности упаковки, которая равна отношению суммарной площади маленьких кругов к площади квадрата/круга.
Скачать Tight packing.rar.
Текст программы на языке Dart (разработчик Бондарев Сергей):