Случайная упаковка шаров — различия между версиями
| Строка 8: | Строка 8: | ||
Для запуска программы выберите, какой эксперимент хотите провести - случайная упаковка в квадрате ( кнопка "square") или в круге (кнопка "circle") и нажмите "старт". | Для запуска программы выберите, какой эксперимент хотите провести - случайная упаковка в квадрате ( кнопка "square") или в круге (кнопка "circle") и нажмите "старт". | ||
| − | Так же мы можем варьировать отношение | + | Так же мы можем варьировать отношение диаметра маленького кружка <math> a </math> к стороне квадрата/диаметру большого круга <math> d </math> и количество экспериментов - <math> n </math>. |
После наших экспериментов мы построили график зависимости удельного числа проводимых экспериментов(т.е. отношение кол-ва экспериментов с данной плотностью к общему числу экспериментов) от плотности упаковки, которая равна отношению суммарной площади маленьких кругов к площади квадрата/круга. | После наших экспериментов мы построили график зависимости удельного числа проводимых экспериментов(т.е. отношение кол-ва экспериментов с данной плотностью к общему числу экспериментов) от плотности упаковки, которая равна отношению суммарной площади маленьких кругов к площади квадрата/круга. | ||
Версия 14:57, 4 мая 2016
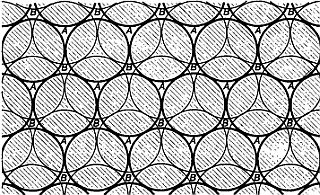
Виртуальная лаборатория > Случайная упаковка шаровРассматривается задача плотной упаковки шаров заданного радиуса в квадрате и круге. Так же в ходе исследования выявляется наиболее плотная 2D упаковка из рассматриваемых.
Для запуска программы выберите, какой эксперимент хотите провести - случайная упаковка в квадрате ( кнопка "square") или в круге (кнопка "circle") и нажмите "старт". Так же мы можем варьировать отношение диаметра маленького кружка к стороне квадрата/диаметру большого круга и количество экспериментов - .
После наших экспериментов мы построили график зависимости удельного числа проводимых экспериментов(т.е. отношение кол-ва экспериментов с данной плотностью к общему числу экспериментов) от плотности упаковки, которая равна отношению суммарной площади маленьких кругов к площади квадрата/круга.
Скачать Tight packing.rar.
Текст программы на языке Dart (разработчик Бондарев Сергей):