Визуализация броуновского движения — различия между версиями
Материал из Department of Theoretical and Applied Mechanics
(→Ссылки) |
|||
| Строка 15: | Строка 15: | ||
За основы была взята программа, разработанная [[Цветков Денис|Цветковым Денисом]] | За основы была взята программа, разработанная [[Цветков Денис|Цветковым Денисом]] | ||
В программу были добавлены периодические граничные условия, а также некоторые настройки. <br> | В программу были добавлены периодические граничные условия, а также некоторые настройки. <br> | ||
| − | Взаимодействие между шарами задаётся [[Потенциал_Леннард-Джонса|потенциалом Леннарда-Джонса]] | + | Взаимодействие между шарами задаётся [[Потенциал_Леннард-Джонса|потенциалом Леннарда-Джонса]] <br> |
[[Файл:MSB_formula.png]] | [[Файл:MSB_formula.png]] | ||
Формула для вычисления среднего квадратичного смещения в двумерном случае, | Формула для вычисления среднего квадратичного смещения в двумерном случае, | ||
| − | где T-- время по которому усредняется , x_0 -- начальная координата. | + | где T-- время по которому усредняется , x_0 -- начальная координата.<br> |
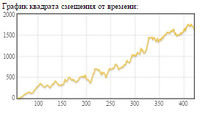
| + | На графике представлен результат работы программы. | ||
| + | [[Файл:SD Graph.jpg|thumb|200px|Графика зависимости квадрата удаления частицы от начальной точки.]] | ||
===Демонстрационная программа=== | ===Демонстрационная программа=== | ||
Версия 08:03, 8 февраля 2016
Виртуальная лаборатория > Визуализация броуновского движенияСодержание
Курсовой проект по механике дискретных сред
- разработчик Опочанский Александр
- руководитель Кузькин Виталий
Цель проекта
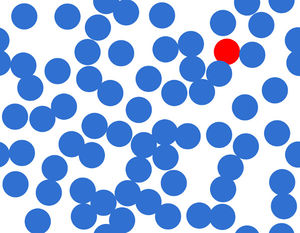
Разработать интерактивную модель поведения частицы в дискретной среде. На полученной модели продемонстрировать процесс случайного блуждания частицы.
Математическая модель и разработка программы
За основы была взята программа, разработанная Цветковым Денисом
В программу были добавлены периодические граничные условия, а также некоторые настройки.
Взаимодействие между шарами задаётся потенциалом Леннарда-Джонса
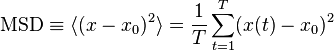 Формула для вычисления среднего квадратичного смещения в двумерном случае,
где T-- время по которому усредняется , x_0 -- начальная координата.
Формула для вычисления среднего квадратичного смещения в двумерном случае,
где T-- время по которому усредняется , x_0 -- начальная координата.
На графике представлен результат работы программы.
Демонстрационная программа
|
Шаг интегрирования:
dt =
/1000 Гравитация:
mg =
⋅ m ⋅ g0 Масса красного шара:
Bmass =
Сколько шаров помещается по вертикали:
Конфигурация:
Short Lennard-Jones potential
Термостат:
T ⋅ T0 =
Разгон случайными скоростями Термостат действует на: Внутреннее трение T ≈
Количество частиц:
скорость обновления:
отладка:
|
График квадрата смещения от времени:
|