Одномерное уравнение теплопроводности. Суранов Ян Сергеевич. 6 курс — различия между версиями
Материал из Department of Theoretical and Applied Mechanics
Ян (обсуждение | вклад) |
Ян (обсуждение | вклад) (→Результаты) |
||
| Строка 32: | Строка 32: | ||
[[File:Безымянный.jpg|thumb|720px|center]] | [[File:Безымянный.jpg|thumb|720px|center]] | ||
| − | *При уменьшении числа узлов в сетки, для данной | + | *При уменьшении числа узлов в сетки, для данной реализации, время расчета увеличивается. |
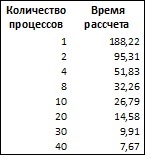
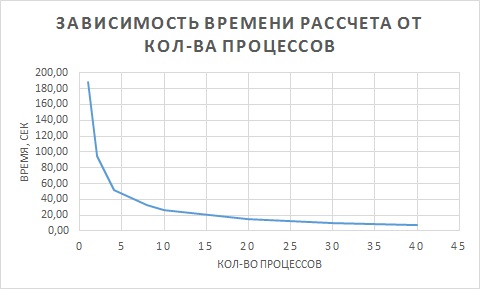
*При увеличении числа процессов время расчета существенно сокращается, что делает целесообразным использование данного метода. | *При увеличении числа процессов время расчета существенно сокращается, что делает целесообразным использование данного метода. | ||
| − | |||
==Полезные ссылки== | ==Полезные ссылки== | ||
[https://ru.wikipedia.org/wiki/%D0%A3%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5_%D1%82%D0%B5%D0%BF%D0%BB%D0%BE%D0%BF%D1%80%D0%BE%D0%B2%D0%BE%D0%B4%D0%BD%D0%BE%D1%81%D1%82%D0%B8 Уравнение теплопроводности] | [https://ru.wikipedia.org/wiki/%D0%A3%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5_%D1%82%D0%B5%D0%BF%D0%BB%D0%BE%D0%BF%D1%80%D0%BE%D0%B2%D0%BE%D0%B4%D0%BD%D0%BE%D1%81%D1%82%D0%B8 Уравнение теплопроводности] | ||
Версия 10:49, 10 декабря 2015
Содержание
Постановка задачи
Решается однородное уравнение теплопроводности на промежутке
С граничными условиями
и начальным распределением температуры
Реализация
Конечно-разностная схема
Задача содержит производную по времени первого порядка и производную по пространственной координате второго порядка. Запишем исходное уравнение в виде
Введем равномерную сетку с шагом разбиения . Шаг по времени назовем Построим явную конечно-разностную схему:
Где, — значение температуры в -ом узле.
Компьютерная реализация
Скачать программу File:Heat_Equation_Yan.zip
Результаты
- При уменьшении числа узлов в сетки, для данной реализации, время расчета увеличивается.
- При увеличении числа процессов время расчета существенно сокращается, что делает целесообразным использование данного метода.