Определение модулей жесткости прямолинейных стержней. — различия между версиями
Анастасия (обсуждение | вклад) (Новая страница: «''Автор работы'': Прокопенко Анастасия <br> ''Научный руководитель'': к. ф.-м. н. Вильчевская Е.…») |
Анастасия (обсуждение | вклад) |
||
| Строка 21: | Строка 21: | ||
<math>\rho_{0}\left(\underline{u}\cdot\underline{\underline{\Theta_{1}}}+\underline{\underline{\Theta_{2}}}\cdot\underline{\psi}\right)=\int\rho\underline{a}\times \underline{u_{3}}dxdy</math> | <math>\rho_{0}\left(\underline{u}\cdot\underline{\underline{\Theta_{1}}}+\underline{\underline{\Theta_{2}}}\cdot\underline{\psi}\right)=\int\rho\underline{a}\times \underline{u_{3}}dxdy</math> | ||
| − | [[Файл:free.jpg| | + | [[Файл:free.jpg|200px|thumb|right|Рис.1]] |
| − | [[Файл:nofree.jpg| | + | [[Файл:nofree.jpg|200px|thumb|right|Рис.2]] |
= Нахождение модуля жесткости при поперечном сдвиге = | = Нахождение модуля жесткости при поперечном сдвиге = | ||
| Строка 30: | Строка 30: | ||
В изогнутом стержне в некоторых местах его происходит растяжение, а в других — сжатие. Растянуты линии на выпуклой стороне изогнутого стержня, а на вогнутой стороне происходит сжатие. Как и в случае пластинок, вдоль длины стержня внутри него существует «нейтральная» поверхность, на которой не происходит ни растяжения, ни сжатия. Она отделяет собой области сжатия от областей растяжения. | В изогнутом стержне в некоторых местах его происходит растяжение, а в других — сжатие. Растянуты линии на выпуклой стороне изогнутого стержня, а на вогнутой стороне происходит сжатие. Как и в случае пластинок, вдоль длины стержня внутри него существует «нейтральная» поверхность, на которой не происходит ни растяжения, ни сжатия. Она отделяет собой области сжатия от областей растяжения. | ||
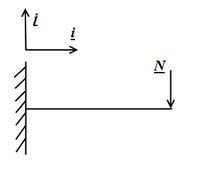
В этой задачи будет две компоненты модуля упругости: на сдвиг и на растяжение. При решении этой задачи нужно раскрыть векторное произведение (см. формула из метода решения). Из-за большого количества узлов погрешность будет большой. Чтобы избежать эту проблему нужно решить две задачи: сдвиг стержня со свободным концом (Рис. 1) и с заделкой, как показано на Рис 2. | В этой задачи будет две компоненты модуля упругости: на сдвиг и на растяжение. При решении этой задачи нужно раскрыть векторное произведение (см. формула из метода решения). Из-за большого количества узлов погрешность будет большой. Чтобы избежать эту проблему нужно решить две задачи: сдвиг стержня со свободным концом (Рис. 1) и с заделкой, как показано на Рис 2. | ||
| + | |||
| + | Угол закручивания в первом случае будет равен: | ||
| + | |||
| + | <math>\underline{\psi _{1}}= \frac{N_{0}}{C_{x}}z\left ( l-\frac{z}{2} \right )\underline{i} </math> | ||
| + | |||
| + | Угол закручивания для стержня с двумя заделками: | ||
| + | |||
| + | <math>\underline{\psi _{2}}= \frac{N_{0}}{C_{x}}\frac{z}{2}\left ( z-l \right )\underline{i} </math> | ||
| + | |||
| + | Выражаем в обоих случаях перемещение, будем иметь соответственно: | ||
| + | |||
| + | <math>u_{1}= -\frac{N_{0}}{A_{y}}z-\frac{N_{0}}{2C_{x}}\left ( z^{2}l-\frac{z^{3}}{3} \right ) </math> | ||
| + | |||
| + | <math>u_{2}= -\frac{N_{0}}{A_{y}}z-\frac{N_{0}}{2C_{x}}\left ( \frac{z^{2}l}{2}-\frac{z^{3}}{3} \right )</math> | ||
| + | |||
| + | Где <math>u_{1}</math> - перемещение стержня со свободным концом, а <math>u_{2}</math> - с заделкой с двух сторон, <math>A_{y}</math> - модуль жесткости на поперечный сдвиг, <math>C_{x}</math> - модуль жесткости на кручение. | ||
| + | Переходим к относительной координате сечения, делая замену <math>r=zl</math>. | ||
| + | Получаем итоговую формулу для модуля жесткости на поперечный сдвиг: | ||
| + | |||
| + | <math>A_{y}=\frac{3rlN_{0}}{u_{1}\left(3-2r\right)-2u_{2}\left(3-r\right)}</math> | ||
| + | |||
| + | = Коэффициент сдвига = | ||
Версия 14:29, 30 ноября 2015
Автор работы: Прокопенко Анастасия
Научный руководитель: к. ф.-м. н. Вильчевская Е.Н.
Содержание
Введение
Теория стержней сыграла большую роль в развитии механики и математической физики. Именно в этой теории впервые возникли дифференциальные уравнения, как обыкновенные, так и в частных производных. В механике сплошных сред, которая описывается уравнениями в частных производных, в которых в качестве независимых переменных выступают три пространственных координаты и время. А в теории стержней фигурируют всего две независимых переменных: одна пространственная координата (обычно длина дуги упругой линии), а второй координатой является время. Получается, что наличие одной пространственной координаты сильно упрощает ситуацию, и именно в теории стержней оказывается возможным исследовать пространственные формы движения. Важно заметить, что тонкий стержень при малых деформациях допускает большие перемещения. Например, изначально прямой стержень можно свернуть в кольцо, при этом деформации стержня останутся пренебрежимо малыми. Существует два метода вывода основных уравнений тонких стержней: асимптотический и прямой. Асимптотический метод основан на уравнениях трехмерной теории и ряде априорных предположений относительно внутренней структуры стержня и характера поведения решения. Прямой метод основан на непосредственном использовании фундаментальных законов механики. Этот метод имеет более широкую область применимости, поскольку при выводе основных уравнений не делается никаких предположений о характере поведения решения, а все особенности внутренней структуры стержня содержатся в тензорах жесткости. В данной работе рассматривается прямой метод.
Цели данной работы
- Определить модули жесткости прямолинейных стержней на основании численного эксперимента
- Исследовать влияние количества сквозных отверстий на модуль жесткости на поперечный сдвиг
Постановка задачи: метод решения
Тензоры жесткости не зависят от деформации, поэтому они могут быть определены по данным линейной теории. Модули упругости будем находить при помощи статического метода. Суть это метода заключается в следующем: решается задача о статическом деформировании по теории стержней, в результате чего находятся перемещения и повороты. Затем та же задача решается по трехмерной теории, либо проводится физический эксперимент, в результате которого также находятся деформации. Важный момент статического метода определения модулей упругости является выбор формул, связывающих между собой характеристики состояния трехмерного тела и состояние соответствующей модели стержня.
Стержень – это модель тонкого трёхмерного тела. Потребуем, чтобы количество движения и кинетический момент у модели и у трёхмерного тела (прообраза) совпадали бы между собой. В результат придём к следующим уравнениям (для линейной теории):
Нахождение модуля жесткости при поперечном сдвиге
Испытания на сдвиг часто используются для оценки механических свойств материалов в хрупком или малопластичном состоянии, при воздействии коррозионной среды (коррозии под напряжением), а также для оценки пластичности и качества сварных соединений. Испытание на сдвиг воспроизводит характерные для многих конструктивных элементов условия механического нагружения и позволяет выявить свойства поверхностных слоев, наиболее напряженных при разрушении.
В изогнутом стержне в некоторых местах его происходит растяжение, а в других — сжатие. Растянуты линии на выпуклой стороне изогнутого стержня, а на вогнутой стороне происходит сжатие. Как и в случае пластинок, вдоль длины стержня внутри него существует «нейтральная» поверхность, на которой не происходит ни растяжения, ни сжатия. Она отделяет собой области сжатия от областей растяжения. В этой задачи будет две компоненты модуля упругости: на сдвиг и на растяжение. При решении этой задачи нужно раскрыть векторное произведение (см. формула из метода решения). Из-за большого количества узлов погрешность будет большой. Чтобы избежать эту проблему нужно решить две задачи: сдвиг стержня со свободным концом (Рис. 1) и с заделкой, как показано на Рис 2.
Угол закручивания в первом случае будет равен:
Угол закручивания для стержня с двумя заделками:
Выражаем в обоих случаях перемещение, будем иметь соответственно:
Где - перемещение стержня со свободным концом, а - с заделкой с двух сторон, - модуль жесткости на поперечный сдвиг, - модуль жесткости на кручение. Переходим к относительной координате сечения, делая замену . Получаем итоговую формулу для модуля жесткости на поперечный сдвиг: