Одномерное уравнение теплопроводности. Буй Ван Шань. 6 курс — различия между версиями
Материал из Department of Theoretical and Applied Mechanics
(→Результаты) |
(→Реализация MPI) |
||
| Строка 12: | Строка 12: | ||
==Реализация MPI== | ==Реализация MPI== | ||
| + | * Данные для расчета | ||
| + | :<math> \begin{cases} | ||
| + | a=0;b=1 | ||
| + | M1(0,t)=6t+0.887 | ||
| + | M2(t)=0.0907 | ||
| + | U0(x)=cos(x+0.48) | ||
| + | f(x,t)=0 | ||
| + | k=1 | ||
| + | \end{cases}</math> | ||
* Скачать [[File:HeatEquation.rar|HeatEquation 2KB]] | * Скачать [[File:HeatEquation.rar|HeatEquation 2KB]] | ||
Версия 02:44, 17 ноября 2015
Постановка задачи
Решается однородное уравнение теплопроводности на промежутке
С граничными условиями
и начальным распределением температуры
- Где f(x,t), U0(x), M1(t), M2(t) - Известные функции
Реализация MPI
- Данные для расчета
- Скачать Файл:HeatEquation.rar
Результаты
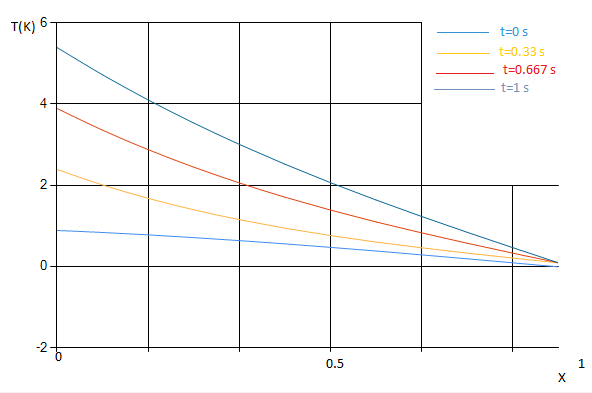
- Решение
- 2 процесса
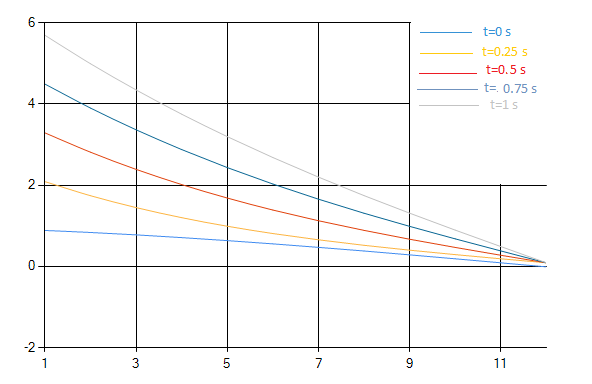
- 4 процесса
- Погрешность вычисления
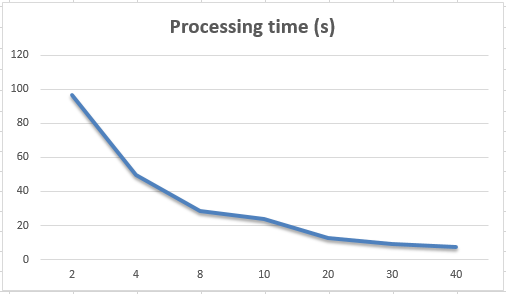
- Зависимость скорости расчета от количества процессов при постоянных шагах вычисления
- Шаг по пространстве dx = 0.0001
- Шаг по времени dt = 0.000001
| Количество процессов | Время рассчета (сек) |
|---|---|
| 2 | 96.58 |
| 4 | 49.4 |
| 8 | 28.66 |
| 10 | 23.63 |
| 20 | 12.89 |
| 30 | 9.27 |
| 40 | 7.52 |
Заметим что при запуске больше количества процессов, скорость расчета быстро снижается