Цилиндр внутри полого цилиндра — различия между версиями
Материал из Department of Theoretical and Applied Mechanics
Foten (обсуждение | вклад) (→top) |
Foten (обсуждение | вклад) |
||
| Строка 13: | Строка 13: | ||
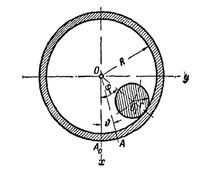
Шероховатый цилиндр массы m и радиуса r катится без скольжения по внутренней поверхности полого цилиндра массы M и радиуса R, могущего вращаться около своей горизонтально расположенной оси O. Моменты инерции цилиндров относительно своих осей равны mr2/2 и MR2. Составить уравнения движения системы и найти их первые интегралы. | Шероховатый цилиндр массы m и радиуса r катится без скольжения по внутренней поверхности полого цилиндра массы M и радиуса R, могущего вращаться около своей горизонтально расположенной оси O. Моменты инерции цилиндров относительно своих осей равны mr2/2 и MR2. Составить уравнения движения системы и найти их первые интегралы. | ||
| + | |||
| + | == Решение == | ||
| + | |||
| + | <math>\frac{d}{dt}\left(\frac{\partial L}{\partial\dot q_i}\right) - \frac{\partial L}{\partial q_i} = 0 </math> | ||
| + | |||
| + | где <math>L</math> - функция Лагранжа | ||
| + | |||
| + | <math>L = T-\Pi </math> | ||
| + | |||
| + | <math>T</math> - кинетическая энергия системы, <math>\Pi</math> - потенциальная энергия системы | ||
| + | |||
| + | Выбрав обобщенные координаты <math>\varphi</math> и <math>\psi</math> получим: | ||
| + | |||
| + | <math> \ddot \psi - \frac{m^{2}(R-r)}{2M(M+m)R} \ddot \varphi = 0</math> | ||
| + | |||
| + | <math> \ddot \varphi - \frac{R}{3(R-r)} \ddot \psi + \frac{2g}{3(R-r)} \sin(\varphi) = 0 </math> | ||
Версия 00:41, 27 июня 2015
Проектная деятельность по информатике > Курсовые проекты Группы 09 2015 > Цилиндр внутри полого цилиндраКурсовой проект по информатике
Исполнитель: Александр Смирнов
Группа: 09 (23604)
Семестр: весна 2015
Условие задачи
Шероховатый цилиндр массы m и радиуса r катится без скольжения по внутренней поверхности полого цилиндра массы M и радиуса R, могущего вращаться около своей горизонтально расположенной оси O. Моменты инерции цилиндров относительно своих осей равны mr2/2 и MR2. Составить уравнения движения системы и найти их первые интегралы.
Решение
где - функция Лагранжа
- кинетическая энергия системы, - потенциальная энергия системы
Выбрав обобщенные координаты и получим: