Эллиптический маятник — различия между версиями
Материал из Department of Theoretical and Applied Mechanics
Павел (обсуждение | вклад) (→Решение частного случая) |
Павел (обсуждение | вклад) (→Решение частного случая) |
||
| Строка 28: | Строка 28: | ||
<math>\frac{d}{dt}\left(\frac{\partial L}{\partial\dot q_i}\right) - \frac{\partial L}{\partial q_i} = 0 </math> | <math>\frac{d}{dt}\left(\frac{\partial L}{\partial\dot q_i}\right) - \frac{\partial L}{\partial q_i} = 0 </math> | ||
| + | |||
| + | где <math>L</math> - функция Лагранжа | ||
| + | <math>L = T-П </math> | ||
== См. также == | == См. также == | ||
Версия 03:40, 26 мая 2015
Задача: С помощью языка программирования JavaScript смоделировать эллиптический маятник.
Содержание
Решение
Используемые библиотеки
- cloudflare.js
- dat.gui.js
- googleapis.js
- orbitControls.js
- stats.js
- trackballControls.js
Возможности программы
- задание скорости раскачивания маятника
- детальное рассмотрение работы с удобного ракурса
- получение рисунка траектории маятника
Решение частного случая
Условия задачи:
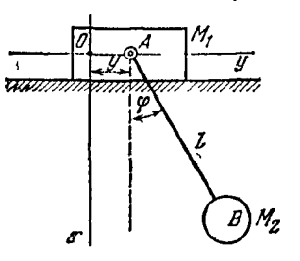
Составить уравнения движения эллиптического маятника, состоящего из ползуна M1 массы m1, скользящего без трения по горизонтальной плоскости, и шарика M2 массы m2, соединенного с ползуном стержнем AB длины l. Стержень может вращаться вокруг оси A, связанной с ползуном и перпендикулярной плоскости рисунка. Массой стержня пренебречь.
Решение:
где - функция Лагранжа