КП: Динамика бильярда — различия между версиями
Павел (обсуждение | вклад) (→Формулировка задачи) |
Павел (обсуждение | вклад) (→Решение) |
||
| Строка 42: | Строка 42: | ||
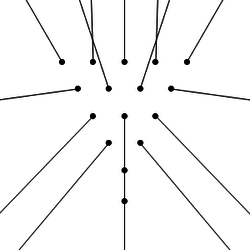
[[Файл:WHVJA1.png|thumb|Траектория разлета шаров при центральном разбиении пирамиды.|250px]] | [[Файл:WHVJA1.png|thumb|Траектория разлета шаров при центральном разбиении пирамиды.|250px]] | ||
| − | [http://mathoverflow.net/questions/156263/perfectly-centered-break-of-a-perfectly-aligned-pool-ball-rack/156407#156407 Профессор Джим Белк (Jim Belk)] рассчитал направление и скорость движения каждого из 15 шаров пирамиды, а также битка , после соударения.Для сравнения, помните, что | + | [http://mathoverflow.net/questions/156263/perfectly-centered-break-of-a-perfectly-aligned-pool-ball-rack/156407#156407 Профессор Джим Белк (Jim Belk)] рассчитал направление и скорость движения каждого из 15 шаров пирамиды, а также битка , после соударения.Для сравнения, помните, что начальная скорость битка была 10 ед/сек. |
[[Файл:017cae37a4318f94cff572023a52bddb.png|слева]] | [[Файл:017cae37a4318f94cff572023a52bddb.png|слева]] | ||
Версия 04:02, 13 мая 2015
А.М. Кривцов > Теоретическая механика > Курсовые проекты ТМ 2015 > Динамика бильярда
Исполнитель: Булдаков Павел
Группа: 09 (23604)
Семестр: весна 2015
Содержание
Аннотация проекта
Данный проект посвящен изучению динамики бильярда .В ходе работы над проектом было рассмотрено разбиение пирамиды из шаров, данный процесс смоделирован на языке JavaScript.
Формулировка задачи
- Написать программу, моделирующую динамику взаимодействия шаров при игре в Бильярд. Взаимодействие между шарами описывается с помощью потенциала Леннарда-Джонса.
-Рассмотреть классическое разбиение в русском бильярде, проследить траекторию разлета.
Общие сведения по теме
Впервые о математическом базисе бильярдной игры заговорил Гаспар Гюстав Кориолис в своей книге «Théorie mathématique du jeu de billard» (Русск. перевод: «Математическая теория явлений бильярдной игры») в 1835 году. Он использовал в своей работе элементы теории вероятностей, теории пределов и общего анализа. Однако особого интереса у современников книга не вызвала: ни у математиков, ни у бильярдистов.
Прошло более полутораста лет, и математический бильярд развился в свою теорию, породив несколько побочных. «Теория бильярдов» сегодня неотъемлемая часть эргодической теории и теории динамических систем, имеет важнейшее применение в физике. Математиком Гальпериным создан способ определения числа pi с помощью бильярда. Намного ближе общеобразованному читателю результаты исследований математиков Штайнхауса, Альхазена и Гарднера.
При реализации данной задачи используется стол с размерами игрового поля 2240 х 1120 мм, диаметром шара 68 мм и размерами луз 72 и 82 мм соответственно.
Решение
Приняты некоторые допущения:
- все шары считаются идеально упругими и почти идеально жёсткими;
- каждый шар имеет массу в 1 единицу и радиус в 1 единицу;
- взаимодействие между двумя шарами описывается формулой
где d — расстояние между центрами шаров, — сила Леннард-Джонса
Профессор Джим Белк (Jim Belk) рассчитал направление и скорость движения каждого из 15 шаров пирамиды, а также битка , после соударения.Для сравнения, помните, что начальная скорость битка была 10 ед/сек.
Ниже приведена программа( созданная совместно со Степановым Матвеем на основании программы Динамика взаимодействующих частиц) , в которой видно, что траектория разлета шаров схожи с расчетными траекториями профессора.
В реальности данная картина так же видна, хоть и не столь явно из-за неидеальности системы .