Вычисление упругих характеристик кристаллических решеток графена и алмаза с применением многочастичных потенциалов — различия между версиями

Версия 16:38, 16 июля 2011

Введение

В настоящее время большое внимание уделяется исследованию упругих свойств кристаллической решетки графена (монослой графита).

В данной работе вычисление модулей упругости кристаллических решеток графена и алмаза ведется аналитически и с помощью компьютерного эксперимента. При вычислении используется метод молекулярной динамики (ММД) ^[1] с применением многочастичного потенциала Терсоффа ^{[2] [3] [4]}, Терсоффа-Бреннера ^{[5] [6]}, а также потенциала Бреннера второго поколения ^[7].

• Аналитические расчеты: И. Е. Беринский
• Компьютерный эксперимент: В. А. Цаплин

Аналитическое вычисление модулей упругости

Квазистатическое вычисление модулей упругости

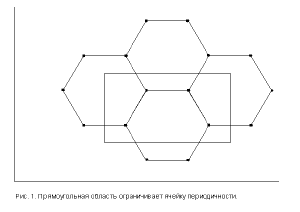
На первом этапе вычисления находится положение равновесия решетки в растянутом состоянии. При этом задается либо растяжение вдоль двух осей симметрии решетки (рис. 1), либо сдвиговая деформация вдоль одной из осей. На этом этапе решается динамическая задача достижения положения равновесия. Компьютерный эксперимент производится посредством вычисления радиус векторов и векторов скорости частиц в зависимости от времени. Интегрирование ведется методом центральных разностей. Метод состоит в том, что координаты и силы вычисляются во временных точках, разделенных интервалами, равными шагу интегрирования, а скорости вычисляются во временных точках, находящихся в серединах вышеупомянутых интервалов:

[math]\underline{v} (t + \tau / 2) = \underline{v} (t - \tau / 2) + \underline{w} (t) \tau[/math]

[math]\underline{r} (t + \tau) = \underline{r} (t) + \underline{v} (t + \tau / 2) \tau,[/math]

где [math]\tau[/math] – шаг интегрирования. Ускорение [math]\underline{w}(t)[/math] вычисляется через приложенную к частице силу.

Для нахождения силы, приложенной к одной частице, рассматриваемая область разбивается на квадратные ячейки со стороной, не меньшей [math]R + D[/math]. Рассматриваются все частицы, находящиеся в одной ячейке, либо в соседних ячейках к ячейке, где находится частица, для которой вычисляется приложенная сила.

Колебания атомов гасятся введением коэффициента трения в уравнения движения. При этом достигается однородное деформированное состояние со значениями [math]\varepsilon_{11} = 0.001[/math] (при растяжении вдоль оси [math]OX_1[/math]), и [math]\varepsilon_{22} = 0.001[/math] (при растяжении вдоль оси [math]OX_2[/math]). При вычислении используется несколько ячеек периодичности и ставятся периодические граничные условия.

Вычислительный процесс разделим на три основные части. Первая часть представляет собой вычислительный процесс в целом и включает в себя определение начальных параметров задачи, которые могут варьироваться, а также определение начальной конфигурации рассчитываемой системы, т.е. границы рассматриваемой области, положение и скорости частиц (атомов) кристаллической решетки. Кроме того, вычислительный процесс в целом подразумевает последовательность шагов интегрирования по времени и получение результатов вычисления. Вторая часть вычислительного процесса представляет собой один шаг интегрирования по времени. Результатом этой части вычислительного процесса является определение наборов соседних атомов для каждого атома системы с учетом граничных условий, т.е. условий периодичности на границе рассматриваемой прямоугольной области. Шаг интегрирования по времени состоит из определения скоростей атомов при учете действующих сил на каждый атом системы, а также определение приращений перемещений атомов системы. Третья часть вычислительного процесса представляет собой определение слагаемых сил, действующих на один атом системы и на соседние с ним атомы. Эта часть содержит вычисление значения производных от одного слагаемого потенциальной энергии системы, т.е. потенциальной энергии, приходящейся на один атом.

На втором этапе механические напряжения в решетке вычисляются по формулам ^[8]:

[math] {{\underline{\underline{\tau\hspace{-0.5mm}}}\hspace{0.5mm}}}_i = \frac{1}{2V} \sum_{\alpha} \underline{F}_{\alpha}^i \underline{A}_{\alpha}^i = \frac{1}{2V} \sum_{\alpha} \underline{F}_{\alpha}^i (\underline{r}_{\alpha}^i - \underline{r}_i), [/math]

иначе

[math] {{\underline{\underline{\tau\hspace{-0.5mm}}}\hspace{0.5mm}}}_i = \frac{1}{V} \sum_{\alpha} \frac{\partial \Pi^i}{\partial \underline{A}_{\alpha}^i} (\underline{r}_{\alpha}^i - \underline{r}_i), \quad \Pi^i = \frac{1}{2} \sum_{j (\neq i)} V_{ij} [/math]

Здесь [math]{{\underline{\underline{\tau\hspace{-0.5mm}}}\hspace{0.5mm}}}_i[/math] – тензор механических напряжений для частицы (атом углерода) с номером [math]i[/math]. При однородном поле деформации находится средний тензор напряжений [math]({{\underline{\underline{\tau\hspace{-0.5mm}}}\hspace{0.5mm}}}_i)[/math] по всем частицам. [math]V[/math] – объем ячейки периодичности (в двумерной постановке – площадь). [math]\underline{F}_{\alpha}^i[/math] – векторный коэффициент, равный [math]\displaystyle 2 \frac{\partial \Pi^i}{\partial \underline{A}_{\alpha}^i}[/math], где [math]\alpha[/math] – номер соседней частицы к частице с номером [math]i[/math]. [math]\underline{A}_{\alpha}^i[/math] – вектор относительного положения соседней частицы: [math]\underline{A}_{\alpha}^i = \underline{r}_{\alpha}^i - \underline{r}_i[/math], где [math]\underline{r}_i[/math] – радиус-вектор частицы с номером [math]i[/math], [math]\underline{r}_{\alpha}^i[/math] – радиус-вектор соседней частицы ([math]\alpha[/math]). [math]V_{ij}[/math] – энергия, приходящаяся на одну связь, см. потенциал Терсофа.

В двумерной постановке (графен) коэффициенты упругости вычисляются с помощью соотношений между компонентами напряжений и деформаций:

[math]\sigma_1 = C_{11} \varepsilon_{11} + C_{12} \varepsilon_{22},\quad[/math]

[math]\sigma_2 = C_{12} \varepsilon_{11} + C_{22} \varepsilon_{22},\quad[/math]

[math]\tau_{12} = 2 C_{44} \varepsilon_{12}[/math].

При этом модули упругости выражаются через эти коэффициенты по формулам:

[math] \nu = \frac{C_{12}}{C_{11}},\quad E = \frac{C_{11}^2 - C_{12}^2}{C_{11}},\quad K = \frac{1}{2}(C_{11} + C_{12}). [/math]

Здесь [math]\nu[/math] – коэффициент Пуассона, [math]E[/math] – модуль Юнга, [math]K[/math] – коэффициент объемного сжатия.

В результате компьютерного эксперимента для графена получены значения, приведенные в таблице 1. Количество цифр соответствует точности вычисления.

В трехмерном ортотропном материале с кубической симметрией (алмаз) коэффициенты упругости определяются через следующие выражения:

[math] \begin{array}{l} \sigma_1 = C_{11} \varepsilon_{11} + C_{12} \varepsilon_{22} + C_{12} \varepsilon_{33},\quad % \sigma_2 = C_{12} \varepsilon_{11} + C_{11} \varepsilon_{22} + C_{12} \varepsilon_{33},\\ % \sigma_3 = C_{12} \varepsilon_{11} + C_{12} \varepsilon_{22} + C_{11} \varepsilon_{33},\\ % \tau_{12} = 2 C_{44} \varepsilon_{12},\quad % \tau_{23} = 2 C_{44} \varepsilon_{23},\quad % \tau_{31} = 2 C_{44} \varepsilon_{31}. \end{array} [/math]

Модули упругости выражаются по формулам:

[math] \nu = \frac{C_{12}}{C_{11} + C_{12}},\quad % E = \frac{(C_{11} - C_{12}) (C_{11} + 2 C_{12})}{(C_{11} + C_{12})},\quad % K = \frac{1}{3}(C_{11} + 2 C_{12}). [/math]

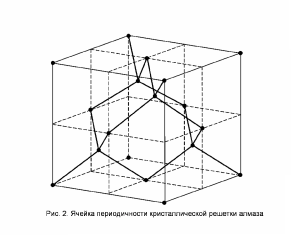
Ячейка периодичности кристаллической решетки алмаза представляет собой куб с гранью [math]4 a_d / \sqrt{3}[/math], где [math]a_d[/math] – межатомное расстояние кристаллической решетки алмаза в равновесном состоянии.

На одну ячейку периодичности приходится 8 атомов углерода (рис. 2), координаты которых в осях, параллельных ребрам куба имеют вид:

Объем такой ячейки равен [math]64\,a_d^3\,/\,3\sqrt{3}[/math], т.е. на один атом приходится объем, равный [math]8\,a_d^3\,/\,3\sqrt{3}[/math]. Результаты вычислений представлены в таблице 2.

Динамическое вычисление модулей упругости

Для вычисления модулей упругости графена динамическим способом находится период гармонических колебаний кристаллической решетки. Форма колебаний задается синусоидальной, кратной длине ячейки периодичности. Рассматриваются два вида колебаний: продольные и поперечные. В обоих случаях отношение пространственного и временного периода колебаний равно скорости распространения соответствующей бегущей волны. Если [math]u_1, u_2[/math] – компоненты вектора смещения частиц, зависящие от координаты [math]x_1[/math], что соответствует распространению волны вдоль оси [math]OX_1[/math], то уравнение продольных колебаний имеет вид:

[math] C_{11} \partial_{11} u_1 = \rho \ddot{u}_1, [/math]

откуда следует выражение для скорости распространения волны:

[math] V^2 = \frac{C_{11}}{\rho} = \left(\frac{l}{T}\right)^2, [/math]

где [math]V[/math] – скорость распространения волны, [math]\rho[/math] – плотность среды, [math]l[/math] – длина волны, [math]T[/math] – период колебаний.

Уравнение поперечных колебаний имеет вид:

[math] C_{44} \partial_{11} u_2 = \rho \ddot{u}_2, [/math]

соответствующее выражение для скорости: [math]\displaystyle V^2 = \frac{C_{44}}{\rho}[/math].

Аналогично, для волн вдоль оси [math]OX_2[/math]:

[math] C_{22} \partial_{22} u_2 = \rho \ddot{u}_2, \quad V^2 = \frac{C_{22}}{\rho}. [/math]

[math] C_{44} \partial_{22} u_1 = \rho \ddot{u}_1, \quad V^2 = \frac{C_{44}}{\rho}. [/math]

Для гармонических колебаний вдоль оси [math]OX_1[/math] с длиной волны [math]l = 219.8 \mbox{\AA}[/math] (50 ячеек периодичности) в ходе компьютерного эксперимента получены значения периода продольных колебаний [math]24.68 \pm 0.01[/math] и периода поперечных колебаний [math]32.36 \pm 0.01[/math]. В качестве единицы времени выбрана величина периода колебаний одного атома в прямой бесконечной цепочке атомов при условии, что другие атомы закреплены. Для колебаний вдоль оси [math]OX_2[/math] с длиной волны [math]l = 253.8 \mbox{\AA}[/math] (100 ячеек периодичности) период продольных колебаний составил [math]28.50 \pm 0.01[/math], период поперечных колебаний [math]37.36 \pm 0.01[/math]. В результате модули упругости получили значения, приведенные в таблицах 3, 4.

Приложение

Таблицы параметров вычислительных экспериментов

Список литературы

1. ↑ А.М.Кривцов, И.Б.Волковец, П.В.Ткачев, В.А.Цаплин, Применение метода динамики частиц для описания высокоскоростного разрушения твердых тел // Математика. Механика. Информатика. Труды конференции, посвященной 10-летию РФФИ. – М. ФИЗМАТЛИТ, 2004. С. 361–377 (1122 Kb)
2. ↑ J.Tersoff, New empirical approach for the structure and energy of covalent system // Phys.Rev. B (1988) V. 37, No 12, P.6991–6999 (2.50 Mb)
3. ↑ J.Tersoff, Empirical Interatomic Potential for Carbon, with Applications to Amorphous Carbon // Phys.Rev. B. 1988. 61, 2879–2882. (708 Kb)
4. ↑ Sakir Erkoc, Empirical many-body potential energy functions used computer simulations of condensed matter properties, Physics Reports 278 (1997), P. 79–105 (937 Kb)
5. ↑ D.W.Brenner. Empirical Potential for Hydrocarbons for Use in Simulating the Chemical Vapor Deposition of Diamond Films // Phys.Rev. B. 1990. V.42, pp. 9458–9471. (2.21 Mb) (errors 102 Kb)
6. ↑ C.D.Reddy, S.Rajendran and K.M.Liew, Equilibrium configuration and continuum elastic properties of finite sized graphene // Nanotechnology, 2006, 17, 864–870.
7. ↑ D.W.Brenner, O.A.Shenderova, J.A.Harrison, S.J.Stuart, B.Ni, S.B.Sinnot. A second-generation reactive empirical bond order (REBO) potential energy expression for hydrocarbons // J.Phys: Condens. Matter 14 (2002), 783–802. (144 Kb)
8. ↑ А.М.Кривцов, Деформирование и разрушение твердых тел с микроструктурой, М: ФИЗМАТЛИТ, 2007, 304 с.