Ибраев Д.Ф.: Исследование динамики удара частиц в присутствии жидкой фазы для описания грануляционных процессов — различия между версиями

Версия 19:04, 19 июня 2014

Описание

Данная работа выполнена в рамках Гамбургского проекта при поддержке стипендиальной программы "Леонард Эйлер" немецкой службы академических обменов (DAAD).

Руководители

Руководитель со стороны СПбГПУ: к.ф.-м.н И.Е. Беринский

Руководители со стороны TUHH: Dipl.-Ing. V. Salikov, Prof. Dr.-Ing. S. Antonyuk

Аннотация

Грануляция традиционно считается эмпирическим искусством с большими трудностями в прогнозировании и объяснении наблюдаемых процессов. Промышленность столкнулась с рядом проблем, включая большой процент утилизации, плохой контроль качества продукции, большие расхождения при переходе от лабораторных гранулирующих устройств к промышленным. При условии, что известны соответствующие свойства материала и рабочие параметры, в настоящее время можно сделать полезные предположения о том, как из порошка формируются гранулы.

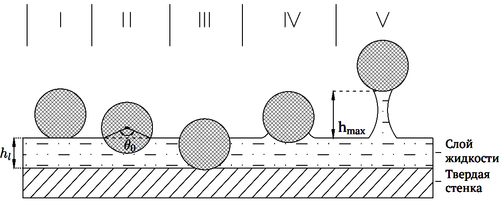
Содержание жидкой фазы при грануляции влияет на свойства столкновений между частицами. Во время этого процесса из-за увлажнения частиц (покрытие частиц жидкой пленкой или каплями) при соударении происходит потеря начальной энергии частиц, которую можно описать с помощью коэффициента восстановления. Реализация соударения двух частиц в лабораторных условиях является технически сложной задачей, поэтому рассматривается удар частицы о смоченную твердую поверхность.

Удар частицы о смоченную твердую поверхность

Данная работа состоит из экспериментальной части, аналитического исследования и численного моделирования. В результате серии экспериментов определены коэффициенты восстановления при прямом ударе частиц о твердую поверхность, покрытую тонким слоем жидкости. Рассматривались удары частиц о смоченную поверхность и сухие удары, варьировались скорость частицы до удара и толщина слоя жидкости. Построена аналитическая модель для определения коэффициента восстановления при ударе. Проведено численное моделирование процесса удара с использованием сопряжения ABAQUS и STAR-CCM+. Результаты аналитического и численного моделирования с достаточно высокой точностью совпадают с экспериментальными данными.

Полученные результаты будут использованы при численном моделировании процесса грануляции с последующей разработкой гранулирующего устройства.

Аналитическая модель

В процессе удара частицы о смоченную поверхность на частицы действуют следующие силы: капиллярная сила, сила вязкости, сила сопротивления, сила при контакте частицы со свободной поверхностью жидкости и твердой поверхностью стенки, сила Архимеда и сила тяжести. При моделировании было принято, что влиянием таких сил, как сила вязкости, сопротивления и Архимеда можно пренебречь, исходя из результатов работы [1].

Периоды удара частицы о смоченную твердую поверхность

Закон сохранения энергии для частицы в процессе удара примет вид:

[math] m_0 u_0^2=m_f u_f^2+2L, [/math]

где [math]u_0, u_f[/math] - скорости частиц до удара и после соответственно, [math]m_0[/math] - масса частицы, [math]m_f=\rho_w V_w+m_0[/math] - суммарная масса частицы и жидкости, присоединенной к частице, [math]V_w=\frac{4}{3}\pi(R+h_w)^3-\frac{4}{3}\pi R^3[/math] - объем жидкости на частице после удара, [math]h_w[/math] - толщина слоя жидкости на частице после удара, [math]L[/math] - потеря энергии при ударе.

Коэффициент восстановления частицы при столкновении со стенкой можно записать следующим образом:

[math] e=-\frac{u_f}{u_0}=\sqrt{\frac{m_0}{m_f}-\frac{2L}{m_f u_0^2}} [/math]

Потеря энергии [math]L[/math]:

[math] L = A_{\text{cap}}+L_l+L_c, [/math]

где [math]A_{\text{cap}}[/math] - работа капиллярных сил, [math]L_l[/math] и [math]L_{\text{c}}[/math] - энергия, затраченная на удар частицы о свободную поверхность жидкости и удар о стенку соответственно.

Жидкий мостик между сферой и стенкой

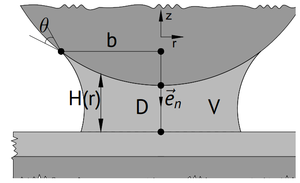
Выражение для капиллярной силы [math]\vec F_{\text{cap}}[/math] было получено в работе [2]. Работа [math]A_{\text{cap}}[/math] выражается следующим образом:

[math] A_{\text{cap}} =\int_0^{h_{max}} \vec{F}_{\text{cap}}d(\vec{e}_{u}D) =\int_0^{h_{max}} 2\pi R \sigma \cos \theta \cdot \left(\displaystyle 1-\frac{1}{\sqrt{1+\frac{2V}{\pi R D^2}}}\right)\vec{e}_n d(\vec{e}_{u}D), [/math]

где [math]D[/math] - расстояние между сферой и стенкой, [math]\sigma[/math] - коэффициент поверхностного натяжения, [math] V = \frac{\pi R}{2} [H^2(b)-D^2][/math] - объем жидкого мостика, [math]b[/math] - радиус смоченной области и [math]H(r)=D+r^2/R[/math].

В научной работе [4] было получено следующее соотношение мгновенной кинетической энергии жидкости, окружающей частицу, при первоначальном контакте в терминах безразмерного времени [math]\tau[/math] и малого параметра [math]\varepsilon[/math][4]: [math] K(\varepsilon)=\frac{4}{3}\rho_w R^3 u_0^2 \varepsilon^3(1-0.35\varepsilon-0.176\varepsilon^2)+O(\varepsilon^6);\\ \tau =u_0 t/R=\displaystyle\frac{\varepsilon^2}{2}+O(\varepsilon^3);\\ \varepsilon(\tau)=\pi-\theta_0(\tau); \tau\ll1, [/math]

где [math]R[/math] - радиус частицы, [math]\rho_w [/math] - плотность жидкости, [math]a = r \sin \theta_0 [/math], [math]\theta_0[/math] - мгновенный угол расположения частицы ниже свободной поверхности жидкости.

При выводе выражения для [math]K(\varepsilon)[/math] было сделано предположение, что на начальной стадии удара частицы о свободную поверхность жидкости инерционные силы доминируют над силами поверхностного натяжения, гравитации, вязкого взаимодействия и эффектов сжимаемости.

Известно, что гидродинамическая нагрузка на частицу, проникающую в жидкость, достигает своего максимума при относительно малых значениях безразмерного времени. В рамках предположений можно считать максимальную кинетическую энергию жидкости вблизи частицы [math]K(\varepsilon)[/math] равным диссипации энергии частицы при ударе о свободную поверхность жидкости:

[math] L_l = \max K(\varepsilon)=K(1.251) [/math]

Потеря энергии при контакте с твердой поверхностью:

[math] L_c = \frac{1}{2}m_0(1-e_c)u_0^2, [/math]

где [math]e_c [/math] - коэффициент восстановления при сухом ударе.

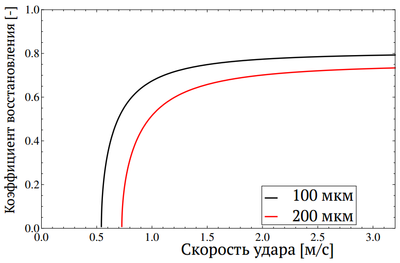
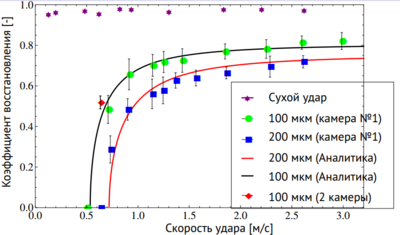
Таким образом, был определен коэффициент восстановления для стеклянного шарика при ударе о стенку, покрытую слоем воды. Коэффициент восстановления растет с увеличением скорости удара и выходит на постоянное значение при определенной скорости. C ростом толщины слоя жидкости коэффициент [math]e [/math] понижается вследствие растяжения жидкого мостика при отскоке.

Параметры моделирования

Результаты моделирования

Эксперимент

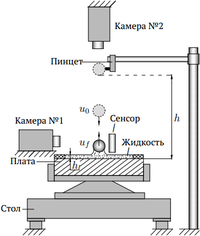
В лаборатории Гамбургского технического университета была собрана экспериментальная установка для определения коэффициента восстановления [math]e[/math].

Схема экспериментальной установки [1]

Перед падением частица закреплена с помощью вакуумного пинцета. Текущая толщина слоя воды контролировалась с помощью конфокального сенсора. Скорости частиц при падении и отскоке были получены с помощью высокоскоростной камеры №1, которая производила съемку с кадровой частотой 8000 к/с области с разрешением 192x176 пикселей. Камера №2 с теми же характеристиками располагается в верхней части установки и фиксирует движение частицы в плоскости платы.

Обработка изображений в Matlab

Обработка изображений, полученных с камер, проводилась с помощью программного кода, написанного в среде MATLAB. Программа была написана сотрудником Гамбургского технического университета (TUHH) S. Antonyuk. В данной работе программа была модернизирована для использования двух камер. Так же были добавлены фильтры по улучшению изображения при обработке и автоматизирован вывод данных. Эта программа импортирует изображения с камер, переводит их в двоичные изображения, вычисляет центр масс и строит траекторию частицы.

Удар частицы при определенной скорости падения и толщине слоя проводился порядка 100 раз и было подсчитано среднее значение [math]e[/math]. На графике вертикальные отрезки представляют собой стандартное отклонение. С увеличением скорости падения частицы коэффициент восстановления растет. Также был найден сухой коэффициент восстановления [math]e_с[/math], который с ростом скорости не меняется. С увеличением толщины слоя жидкости величина [math]e[/math] значительно уменьшается. Это вызвано более длительной диссипацией энергии при погружении в слой и растяжением жидкого мостика.

Аналитические результаты хорошо согласуются с экспериментальными данными. Было получено, что расхождения составляют не более 5%, поэтому аналитическую модель можно использовать при анализе задачи в описанной постановке.

Результаты эксперимента и аналитической модели

Численное моделирование

Проведено численное моделирование процесса удара с использованием сопряжения ABAQUS и STAR-CCM+, что позволило учесть такие эффекты, как смачивание частицы, вязкость жидкости, сила сопротивления и сила Архимеда.

Взаимодействие частицы с жидкостью в численной модели

В ABAQUS моделировался удар частицы о твердую поверхность. Для уменьшения времени вычисления был рассмотрен сектор шара с заданными на плоских гранях условиями симметрии. Были заданы следующие условия: начальная скорость падения шара, условие гравитации и контактное взаимодействие шара и стенки. Количество элементов в модели составляло 2162.

Модель в Abaqus

Модель в Star

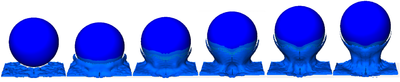
В STAR-CCM+ была построена модель взаимодействия частицы с жидкостью. Для моделирования свободной поверхности жидкости был использован метод объема жидкости (VOF), определяющий взаимодействие воздуха и воды. В модели были созданы две области: сектор полого шара и область для жидкости. Между этими областями создается интерфейс перекрывающейся сетки. Это объемный тип интерфейса, который обеспечивает соединение решений расчетных областей, используя автоматически создаваемый набор замещаемых ячеек в одной области и замещающих в другой. Переменные величины в заменяемых ячейках замещаются переменными величинами в заменяющих ячейках, используя интерполяцию. Так же как и в ABAQUS, в STAR-CCM+ решается симметричная задача: условия симметрии на плоских гранях шара и на двух границах области жидкости. На внутреннюю поверхность полого шара задаются условие стенки и перемещения, полученные с ABAQUS. Эта поверхность будет взаимодействовать с жидкостью. На внешнюю поверхность шара задается условие перекрывающейся сетки. На остальных поверхностях шара задается условие ”плавающей” динамической сетки, которая позволяет поверхностям двигаться вместе с шаром. На нижней границе области жидкости задается условие стенки, на остальных границах — условие плоской волны. Количество расчетных элементов в модели составляло 164000, количество итераций 20, временной шаг сопряжения e-5 c.

В ABAQUS моделировался удар частицы о твердую поверхность, в STAR-CCM+ – взаимодействие частицы с жидкостью. В качестве материала использовалось стекло:[math]\rho_p=2500[/math] кг/м[math]^3[/math], [math]E=71.4[/math] ГПа, [math]\nu=0.25[/math].