КП: Кинематика кривошипно-шатунного механизма — различия между версиями
Влад (обсуждение | вклад) |
Влад (обсуждение | вклад) |
||
| Строка 39: | Строка 39: | ||
При повороте кривошипа на угол φ перемещение поршня от его начального положения в ВМТ определяется отрезком АА1 и равно: Sп = AA1 = A1O− AO = A1O − (OC + CA) .<br> | При повороте кривошипа на угол φ перемещение поршня от его начального положения в ВМТ определяется отрезком АА1 и равно: Sп = AA1 = A1O− AO = A1O − (OC + CA) .<br> | ||
<br> <math> S= R+L-(rcos\varphi+Lcos\beta )=r\left [ 1+L/R-(cos\varphi+L/Rcos\beta ) \right ]=r\left [( 1-cos\varphi ) +1/\lambda (1-cos\beta )\right ] </math> | <br> <math> S= R+L-(rcos\varphi+Lcos\beta )=r\left [ 1+L/R-(cos\varphi+L/Rcos\beta ) \right ]=r\left [( 1-cos\varphi ) +1/\lambda (1-cos\beta )\right ] </math> | ||
| − | <br> <math> sin\beta =r/L*sin\varphi=\lambda sin\varphi <math> | + | <br> <math> sin\beta =r/L*sin\varphi=\lambda sin\varphi </math> |
<br> Следовательно, <math> cos\beta =\sqrt{s1-sin^2\beta }=\sqrt{1-\lambda ^2sin^2\varphi} =(1-\lambda ^2sin^2\varphi )^{1/2} <math> | <br> Следовательно, <math> cos\beta =\sqrt{s1-sin^2\beta }=\sqrt{1-\lambda ^2sin^2\varphi} =(1-\lambda ^2sin^2\varphi )^{1/2} <math> | ||
| − | <br> т.к. <math> cos\beta =1-1/2*\lambda ^2sin^2\varphi <math> | + | <br> т.к. <math> cos\beta =1-1/2*\lambda ^2sin^2\varphi </math> |
| − | <br> <math> S=r\left [ (1-cos\varphi )+\lambda /2*sin^2 \right \varphi ]<math>, но т.к. <math> sin^2\varphi =\frac{1-cos2\varphi }{2} <math>, то | + | <br> <math> S=r\left [ (1-cos\varphi )+\lambda /2*sin^2 \right \varphi ]<math>, но т.к. <math> sin^2\varphi =\frac{1-cos2\varphi }{2} </math>, то |
| − | <br> <math> S=r\left [ (1-cos\varphi)+\lambda /4*(1-cos2\varphi ) \right ] <math> - это выражение описывает перемещение поргня в зависимости от угла поворота кривошипа и геометрических размеров КШМ | + | <br> <math> S=r\left [ (1-cos\varphi)+\lambda /4*(1-cos2\varphi ) \right ] </math> - это выражение описывает перемещение поргня в зависимости от угла поворота кривошипа и геометрических размеров КШМ |
Версия 13:18, 23 мая 2014
А.М. Кривцов > Теоретическая механика > Курсовые проекты 2014 > Кинематика кривошипно-шатунного механизма
Курсовой проект по Теоретической механике
Исполнитель: Cолодовников Владислав
Группа: 08 (23604)
Семестр: весна 2014
Аннотация проекта
Данный проект посвящен Кинематическому анализу движения кривошипно-шатунного механизма в двигателе внутреннего сгорания. Кривошипно-шатунный механизм (КШМ) предназначен для преобразования возвратно-поступательного движения поршня во вращательное движение (например, во вращательное движение коленчатого вала в двигателях внутреннего сгорания), и наоборот.
Постановка задачи
- Установление законов движения поршня и шатуна при известном законе движения кривоши-
па.
- Составить уравнения перемещения, ускорения и скорости поршня и шатуна
Постановка задачи
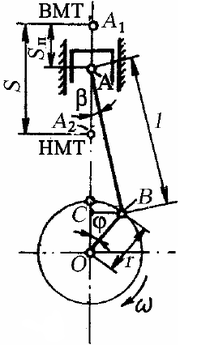
Дан центральный кривошипно-шатунный механизм, у которого ось цилиндра пересекается с осью коленчатого вала.
Примем следующие обозначения:
φ — угол поворота кривошипа в рассматриваемый момент времени
При φ =0 поршень занимает крайнее положение А1 – ВМТ
При φ =180° поршень занимает положение A2 – НМТ
β – угол отклонения оси шатуна
ω= πn/30 – угловая скорость вращения кривошипа
r = OB – радиус кривошипа
L = AB — длина шатуна
λ = r/L – безразмерный параметр КШМ
S = 2r = A1A2 — полный ход поршня
Решение
Перемещение поршня:
При повороте кривошипа на угол φ перемещение поршня от его начального положения в ВМТ определяется отрезком АА1 и равно: Sп = AA1 = A1O− AO = A1O − (OC + CA) .
Следовательно,
, то
- это выражение описывает перемещение поргня в зависимости от угла поворота кривошипа и геометрических размеров КШМ