Ольга Бразгина: Моделирование деформирования твердых гранулированных частиц: влияние формы на деформационное поведение — различия между версиями
(→Моделирование сжатие гранул эллипсоидальной формы) |
(→Моделирование сжатие гранул эллипсоидальной формы) |
||
| Строка 33: | Строка 33: | ||
{|align="center" | {|align="center" | ||
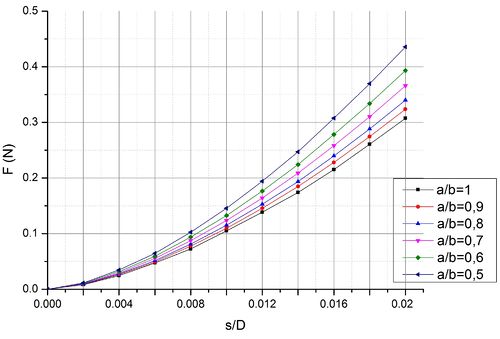
|[[Файл:ell_compare.jpg|500px|thumb|right| Зависимость силы F от перемещения s для частицы в горизонтальном положении]] | |[[Файл:ell_compare.jpg|500px|thumb|right| Зависимость силы F от перемещения s для частицы в горизонтальном положении]] | ||
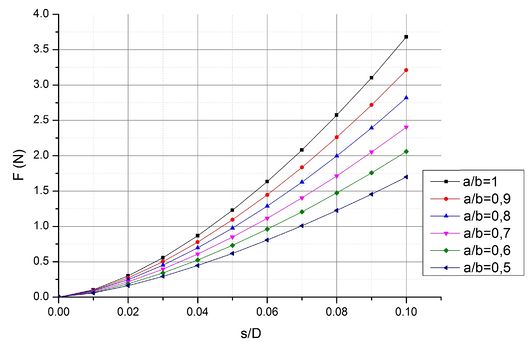
| − | |[[Файл:ell-vert-compare.jpg| | + | |[[Файл:ell-vert-compare.jpg|530px|thumb|right| Зависимость силы F от перемещения s для частицы в вертикальном положении]] |
|} | |} | ||
Версия 22:11, 19 июня 2013
Содержание
Описание
Данная работа выполняется в рамках Гамбургского проекта при поддержке стипендиальной программы "Леонард Эйлер" немецкой службы академических обменов (DAAD).
Участники
Стипендиат: О. Бразгина
Руководители со стороны СПбГПУ: А.М. Кривцов, В.А. Кузькин
Руководители со стороны TUHH: S. Heinrich, S. Antonyuk
Аннотация
Зачастую форма гранулированных частиц существенно отличается от сферической. Существующие на данный момент аналитические модели контактного взаимодействия не позволяют учитывать многие особенности деформирования, ограничиваясь лишь наиболее простыми предположениями.
В частности, не существует теории, описывающей более сложную по сравнению со сферической геометрию частицы. Численное моделирование предоставляет большое поле деятельности путем простого варьирования различных параметров модели, учет тех или иных необходимых свойств, что несравнимо сложнее при аналитическом подходе. Поэтому рассмотрение влияния геометрии частиц путем численного моделирования является необходимым. Моделирование деформационного поведения частиц эллипсоидальной формы позволяет более точно описать отклик частиц неправильной формы, т.к. частиц эллипсоидальной формы являются наиболее простыми несферическими частицами. Моделирование частиц, обладающих внутренней полостью, необходимо для оценки ее прочностных характеристик, которые накладывают ограничение на использование таких гранул.
В данной работе рассматривается упругое, упругопластическое деформирование и разрушение частиц эллипсоидальной формы, а также частиц, обладающих внутренней полостью, определяются зависимости откликов для частиц несферической формы от отклика частиц сферической формы, анализируются критические параметры разрушения частиц.
Моделирование сжатие гранул эллипсоидальной формы
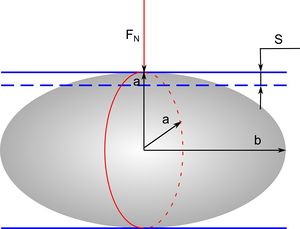
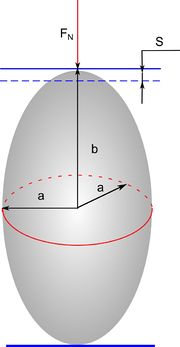
При различном соотношении полуосей эллипсоида a и b проведено моделирование в конечно-элементном пакете ABAQUS 6.11-2. Радиус сферической частицы был задан равным 25 мкм, полуоси частиц для других экспериментов были заданы таким образом, чтобы объем частиц был одинаковым и совпадал с объемом сферы. При этом соотношения полуосей менялось от 1 (соответствует сфере) до 0.5. Материал принят изотропно-упругим ( МПа, ), коэффициент трения между частицей и обкладкой принят равным ). Результаты, полученные для сферической частицы, как показано ранее, близки к аналитическому решению задачи Герца (Механика контактного взаимодействия). Задача решалась в трехмерной постановке, построенная сетка конечных элементов имеет сгущение вблизи области контакта частицы и сжимающей обкладки.
В ходе решения статической задачи были получены поля перемещений, напряжений, а также значения силы контактного взаимодействия. Качественно распределение полей напряжений в эллипсоиде соответствует решению задачи Герца, однако силы, полученные в данном случае несколько отличаются от решения упругой задачи: силы при сжатии эллипсоида несколько больше сил, полученных при сжатии частицы сферической формы, при сжатии частицы в горизонтальном положении, и меньше - в вертикальном. Кроме того, прослеживается зависимость изменения силы от соотношения полуосей эллипсоида.
Для аналитического описания силы сжатия частицы эллипсоидальной формы в обоих случаях были построены соотношения, описывающие связь силы сжатия эллипсоида и силы сжатия сферической частицы. В случае горизонтально расположенной частицы она определяется выражением:
а в случае вертикально расположенной -
Для проверки полученных зависимостей проведено моделирование с целью исследования влияния материальных и геометрических параметров модели. Отмечено небольшое влияние коэффициента Пуассона на отклик частицы. Результаты моделирования, полученные при различных значениях этого коэффициента. Максимальное отличие данных, полученных в ходе моделирования и при аппроксимации - всего 6% - получено при значении коэффициента Пуассона .