КП: Энергия падения метеорита — различия между версиями
Алёна (обсуждение | вклад) (→Общие сведения по теме) |
Алёна (обсуждение | вклад) |
||
| Строка 37: | Строка 37: | ||
<math> E=8,12\cdot 10^8</math> Дж. | <math> E=8,12\cdot 10^8</math> Дж. | ||
| + | |||
| + | Энергия распада урана: рассмотрим реакцию деления ядра урана-235. Ядро делится на два или 3 осколка (зависит от типа реакции)с меньшей суммарной массой с испусканием двух или трёх нейтронов. | ||
| + | |||
| + | Масса атома урана:235,043929 а.е.м. | ||
| + | |||
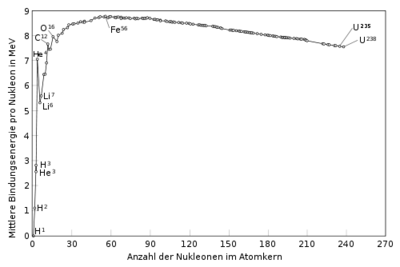
| + | Энергия связи в зависимости от атомного номера | ||
| + | [[Файл:500px-Binding_energy_curve_-_common_isotopes_DE.png|400px|thumb|left|]] | ||
| + | |||
| + | У этих ядер, как видно из таблицы, приведённой выше, удельная энергия связи порядка 8,5 МэВ/нуклон. Удельная энергия связи ядра урана 7,6 МэВ/нуклон. Следовательно, при делении ядра урана выделяется энергия, равная 0,9 МэВ/нуклон или около 205 МэВ на один атом урана, что составляет порядка 1 процента от массы атома урана. | ||
| + | |||
| + | Пример: | ||
| + | Реакция деления ядра урана-235 при столкновении с медленным нейтроном. | ||
| + | |||
| + | [[Файл:UraniumDecay.png]] | ||
Энергия распада урана: | Энергия распада урана: | ||
| − | |||
<math>E=\Delta m\cdot c^2</math>, | <math>E=\Delta m\cdot c^2</math>, | ||
где <math>\Delta m</math> — дефект масс (разность масс ядра и типичных продуктов распада). | где <math>\Delta m</math> — дефект масс (разность масс ядра и типичных продуктов распада). | ||
| − | + | Коэффициент взаимосвязи массы и энергии — | |
| + | |||
| + | с2 = E/m = 8,9874 • 1016 Дж/кг = 931,5 МэВ/а. е. м. | ||
| − | При | + | При этом масса целого ядра до деления больше массы получившихся осколков. Разница составляет примерно 0.1 % массы разделившегося ядра, следовательно, в энергию переходит 0,1 % от первоначальной массы, т.е.,в рассматриваемом случае, 0, 001 кг. |
| − | <math>\Delta m</math> для урана-235 = <math>40 920,5 </math> КэВ | + | <math>\Delta m</math> для урана-235 = <math>40 920,5 </math> КэВ. |
Тогда для ядерной реакции: <math>E=5,9\cdot 10^5</math> Дж. | Тогда для ядерной реакции: <math>E=5,9\cdot 10^5</math> Дж. | ||
| + | |||
== Обсуждение результатов и выводы == | == Обсуждение результатов и выводы == | ||
Версия 19:28, 3 июня 2013
А.М. Кривцов > Теоретическая механика > Курсовые проекты 2013 > Энергия падения метеорита
Курсовой проект по Теоретической механике
Исполнитель: Осокина Алена
Группа: 07 (20510)
Семестр: весна 2013
Содержание
Аннотация проекта
Проект посвящён исследованию энергии, выделяющейся при падении меторита в сопоставлении с другими наиболее известными источниками энергии высоких порядков.
Постановка задачи
1) Сравнить энергию, выделившуюся при столкновении метеорита с Землей с энергией ядерного распада.
2) Сравнить её же с энергией термоядерных реакций.
3) Установить, какие параметры вносят наибольший вклад в то, насколько большой будет выделившаяся энергия (высота падения, масса метеорита, etc)
Общие сведения по теме
Согласно теории относительности, масса представляет собой особую форму энергии, о чем и свидетельствует известная формула Эйнштейна . Из нее следует возможность преобразования массы в энергию и энергии в массу. В частности, часть массы атомного ядра может превращаться в энергию, и происходит это двумя путями. Во-первых, крупное ядро может распасться на несколько мелких — такой процесс называется реакцией распада. Во-вторых, несколько более мелких ядер могут объединиться в одно более крупное — это так называемая реакция синтеза. Реакции ядерного синтеза во Вселенной распространены очень широко — достаточно упомянуть, что именно из них черпают энергию звезды. Ядерный распад сегодня служит одним из основных источников энергии для человечества — он используется на атомных электростанциях. И при реакции распада, и при реакции синтеза совокупная масса продуктов реакции меньше совокупной массы реагентов. Эта-то разница в массе и преобразуется в энергию по формуле
Решение
Рассмотрим падение метеорита весом в 1 кг со 2-ой космической скоростью.
Энергию, выделившуюся при падении метеорита можно считать равной кинетической энергии:
( — 2-ая космическая скорость=11,2 км/с)
Дж.
Энергия распада урана: рассмотрим реакцию деления ядра урана-235. Ядро делится на два или 3 осколка (зависит от типа реакции)с меньшей суммарной массой с испусканием двух или трёх нейтронов.
Масса атома урана:235,043929 а.е.м.
Энергия связи в зависимости от атомного номера
У этих ядер, как видно из таблицы, приведённой выше, удельная энергия связи порядка 8,5 МэВ/нуклон. Удельная энергия связи ядра урана 7,6 МэВ/нуклон. Следовательно, при делении ядра урана выделяется энергия, равная 0,9 МэВ/нуклон или около 205 МэВ на один атом урана, что составляет порядка 1 процента от массы атома урана.
Пример: Реакция деления ядра урана-235 при столкновении с медленным нейтроном.
Энергия распада урана: ,
где — дефект масс (разность масс ядра и типичных продуктов распада).
Коэффициент взаимосвязи массы и энергии —
с2 = E/m = 8,9874 • 1016 Дж/кг = 931,5 МэВ/а. е. м.
При этом масса целого ядра до деления больше массы получившихся осколков. Разница составляет примерно 0.1 % массы разделившегося ядра, следовательно, в энергию переходит 0,1 % от первоначальной массы, т.е.,в рассматриваемом случае, 0, 001 кг.
для урана-235 = КэВ.
Тогда для ядерной реакции: Дж.
Обсуждение результатов и выводы
Как видно из результатов, приведённых выше, энергия, выделившаяся при падении метеорита массой в 1 кг со 2-ой космической скоростью будет на 3 порядка выше, чем энергия ядерного распада 1 кг урана-235.
Для сравнения: энергия взрыва — от 13 до 18 килотонн в тротиловом эквиваленте. Энергия падения метеорита массой в 1 кг — килотонн. Соответственно, при столкновении с Землёй метеорита массой в 100 т произойдёт взрыв, превышающий по значению выделившейся энергии взрыв бомбы в Хиросиме. [[1]]
Ссылки по теме
- Новости науки и техники (падение метеорита под Челябинском)
- [[2]]