КП: Динамика молекулы (расчет) — различия между версиями
Polina (обсуждение | вклад) (→Общие сведения по теме) |
Polina (обсуждение | вклад) (→Решение) |
||
| Строка 50: | Строка 50: | ||
Сфера Хилла рассчитывалась исходя из представлений о точках Лагранжа.Точки Лагранжа-это точки в системе из двух массивных тел, в которых третье тело с пренебрежимо малой массой, на которое не действуют никакие другие силы, кроме гравитационных сил со стороны двух первых тел, может оставаться неподвижным относительно этих тел. | Сфера Хилла рассчитывалась исходя из представлений о точках Лагранжа.Точки Лагранжа-это точки в системе из двух массивных тел, в которых третье тело с пренебрежимо малой массой, на которое не действуют никакие другие силы, кроме гравитационных сил со стороны двух первых тел, может оставаться неподвижным относительно этих тел. | ||
В связи с тем, что для того, чтобы построить эквипотенциальную поверхность с нулевым потенциалом вокруг Земли(а это и есть сфера Хилла), необходимо опираться на сложный математический аппарат, были использованы уже вычисленные значения для геометрического места точек Лагранжа. 1 и 2 точки лежат на прямой,соединяющей центры Земли и Солнца по разную сторону от Земли. Поэтому расстояние от 1 до 2 точки Лагранжа можно считать диаметром сферы Хилла. | В связи с тем, что для того, чтобы построить эквипотенциальную поверхность с нулевым потенциалом вокруг Земли(а это и есть сфера Хилла), необходимо опираться на сложный математический аппарат, были использованы уже вычисленные значения для геометрического места точек Лагранжа. 1 и 2 точки лежат на прямой,соединяющей центры Земли и Солнца по разную сторону от Земли. Поэтому расстояние от 1 до 2 точки Лагранжа можно считать диаметром сферы Хилла. | ||
| − | В случае для Земли масса Земли много меньше массы Солнца, поэтому 1 и 2 точка лежат на примерно одинаковом расстоянии от Земли, и можно считать, что <math>r \approx R \sqrt[3]{\frac{ | + | В случае для Земли масса Земли много меньше массы Солнца, поэтому 1 и 2 точка лежат на примерно одинаковом расстоянии от Земли, и можно считать, что <math>r \approx R \sqrt[3]{\frac{M_{earth}}{3 M_{sun}}}</math> |
== Обсуждение результатов и выводы == | == Обсуждение результатов и выводы == | ||
Версия 11:21, 28 мая 2013
А.М. Кривцов > Теоретическая механика > Курсовые проекты 2013 > Моделирование образования Земли и Луны в газопылевом облаке с учётом солнечного притяжения (расчет)
Курсовой проект по Теоретической механике
Исполнитель: Григорьева Полина
Группа: 07 (20510)
Семестр: весна 2013
Содержание
Аннотация проекта
Данный проект является продолжением работы над Проект "Земля - Луна", начатый А.М.Кривцовым и А.А, Ле-Захаровым. Исследуется поведение газопылевого облака в гравитационном поле, создаваемом Солнцем. Уже получены результаты для облака, имеющего форму эллипсоида. Результатом является образование двойной системы путём одновременного возникновения двух небесных тел, одно из которых в несколько раз больше другого по размеру. Для этого случая были проведены исследования, которые выявили наиболее оптимальные начальные данные, при которых образование двойной системы происходит с большой вероятностью.
Постановка задачи
Выполнить предварительные расчёты и теоретически предсказать результаты моделирования.
Общие сведения по теме
Луна движется не только под влиянием Земли, но и под влиянием Солнца. Однако при этом она остаётся спутником Земли, т.е. находится в области её гравитационного влияния, преобладающего над влиянием Солнца.
В астрономии используется три вида гравитационных сфер: сфера притяжения, сфера действия и сфера Хилла.
Сфера притяжения - такая сфера, в которой гравитационная сила, действующая на спутник со стороны Земли, больше гравитационной силы со стороны Солнца.
Сфера действия - такая сфера, в которой влияние Земли на ускорение спутника значительнее, чем влияние Солнца. Эта сфера не несёт особого физического смысла, однако внутри этой сферы удобнее пользоваться уравнениями в системе отчёта,связанной с Землей, а вне этой сферы - в системе отсчёта, связанной с Солнцем.
Сфера Хилла - область пространства с центром в притягивающей точке - Земле, двигаясь внутри которой тело всегда будет оставаться спутником Земли.[1]
Таким образом, можно сделать вывод: в результате моделирования Луна должна находиться в области пространства, ограниченной сферой притяжения и сферой Хилла.
Действительные радиусы сфер и радиус орбиты Луны:
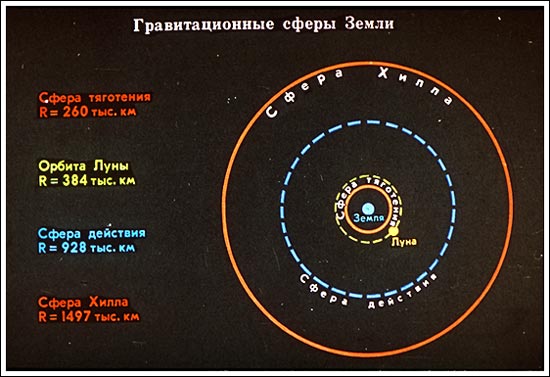картинка взята с сайта [2]
Решение
Введем общие обозначения: , a-расстояние от Земли до Солнца.
- Сфера притяжения
Ищется геометрическое место точек, в которых сила,действующая на спутник в этой точке со стороны Земли больше,чем со стороны Солнца. Фигурой, удовлетворяющей этому условию,является сфера, с центром в точке, отстоящей от точки, в которой располагается Земля, на расстояние (точка лежит на прямой, соединяющей центры Земли и Луны) и радиусом . Для Земли расстояние от центра Земли до центра сферы притяжения на несколько порядков меньше,чем радиус сферы притяжения, поэтому им можно пренебречь и считать центром сферы притяжения центр Земли.
- Сфера действия
Привяжем систему отсчёта к Земле. Тогда ускорение спутника можно разбить на 2 составляющие: в одну в качестве коэффициента входит масса Солнца, в другую - всё остальное. Первую составляющую назовём "возмущающим" ускорением, вторую-"собственным". Отношение этих двух величин обозначим за A1. Чем меньше значение А, тем меньше орбита спутника отличается от Кеплеровской орбиты. Аналогичный коэффициент А2 можем получить,привязав СО к Солнцу. В этом случае "возмущающим" ускорением будет составляющая, в коэффициент при которой входит масса Земли. Область,в которой А1<А2, называется сферой действия Земли относительно Солнца. Геометрическим местом всех таких точек является поверхность, задаваемая уравнением Строго говоря,эта поверхность не является сферой, а представляет собой некоторую "дыню". Однако при малых значениях k поверхность мало отличима от сферы радиусом с центром в точке, совпадающей с центром Земли.
- Сфера Хилла
Сфера Хилла рассчитывалась исходя из представлений о точках Лагранжа.Точки Лагранжа-это точки в системе из двух массивных тел, в которых третье тело с пренебрежимо малой массой, на которое не действуют никакие другие силы, кроме гравитационных сил со стороны двух первых тел, может оставаться неподвижным относительно этих тел. В связи с тем, что для того, чтобы построить эквипотенциальную поверхность с нулевым потенциалом вокруг Земли(а это и есть сфера Хилла), необходимо опираться на сложный математический аппарат, были использованы уже вычисленные значения для геометрического места точек Лагранжа. 1 и 2 точки лежат на прямой,соединяющей центры Земли и Солнца по разную сторону от Земли. Поэтому расстояние от 1 до 2 точки Лагранжа можно считать диаметром сферы Хилла. В случае для Земли масса Земли много меньше массы Солнца, поэтому 1 и 2 точка лежат на примерно одинаковом расстоянии от Земли, и можно считать, что
