Краморов Данил. Курсовой проект по теоретической механике — различия между версиями
Данил (обсуждение | вклад) (→Решение) |
Данил (обсуждение | вклад) (→Решение) |
||
| Строка 17: | Строка 17: | ||
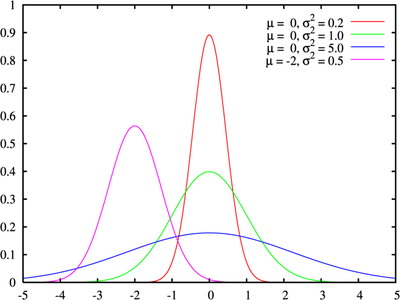
[[Файл:Norm.png|thumb|400px|right| Распределение Гаусса]] | [[Файл:Norm.png|thumb|400px|right| Распределение Гаусса]] | ||
| − | Задача сводится к нахождению функции, описывающей скорость шара в вертикальном воздушном потоке. Найти требуемую функцию можно разными способами. Максимальная скорость (5.6 м/с, расчет был произведен в эксперименте, изучающем закон Бернулли) будет достигаться в центре потока. По краям же скорость будет меньшей. Следовательно в грубом приближение функция скорости будет повторять функцию распределения вероятностей (нормальное распределение, распределение Гаусса). Функция | + | Задача сводится к нахождению функции, описывающей скорость шара в вертикальном воздушном потоке. Найти требуемую функцию можно разными способами. Максимальная скорость (5.6 м/с, расчет был произведен в эксперименте, изучающем закон Бернулли) будет достигаться в центре потока. По краям же скорость будет меньшей. Следовательно в грубом приближение функция скорости будет повторять функцию распределения вероятностей (нормальное распределение, распределение Гаусса). Функция плотности распределения имеет вид: |
| + | <br> | ||
| + | <br> | ||
| + | <math>f(x)= \frac{1} {\sigma \sqrt{2\pi}} e^{-\frac{(x- \mu)^2} {\sigma^2}}</math><br> | ||
| + | <br> | ||
| + | <math> \mu</math> - коэффициент сдвига (вещественное число)<br> | ||
| + | <math> \sigma</math> - коэффициент масштаба (вещественный, строго положительный)<br> | ||
== Обсуждение результатов и выводы == | == Обсуждение результатов и выводы == | ||
Версия 14:10, 26 мая 2012
Содержание
Тема проекта
Колебания шарика в вертикальном воздушном потоке
Постановка задачи
Тело - в данном эксперименте шарик для настольного тенниса - помещается на край вертикального воздушного потока (создается феном). Подчиняясь закону Бернулли, шарик будет пытаться стабилизироваться в центре потока, совершая колебания. Требуется найти уравнение колебаний шарика. Рассматриваются только горизонтальные колебания внутри потока.
Решение
Рассмотрим второй закон Ньютона. В горизонтальном направление на шарик действуют только две силы: подъемная сила (объясняемая эффектом Магнуса) и сила аэродинамического сопротивления.
— плотность жидкости
— скорость шара
A — поперечная площадь шара
Cl — коэффициент подъёмной силы
Задача сводится к нахождению функции, описывающей скорость шара в вертикальном воздушном потоке. Найти требуемую функцию можно разными способами. Максимальная скорость (5.6 м/с, расчет был произведен в эксперименте, изучающем закон Бернулли) будет достигаться в центре потока. По краям же скорость будет меньшей. Следовательно в грубом приближение функция скорости будет повторять функцию распределения вероятностей (нормальное распределение, распределение Гаусса). Функция плотности распределения имеет вид:
- коэффициент сдвига (вещественное число)
- коэффициент масштаба (вещественный, строго положительный)