Моделирование взрыва в SPH постановке — различия между версиями

Материал из Department of Theoretical and Applied Mechanics
Перейти к: навигация, поиск
(→‎Постановка задачи)
Строка 38: Строка 38:
 
Уравнением состоянием было выбрано уравнение Джонсона-Вилкинса-Ли (Jones-Wilkins-Lee). Используется для точного описания поведения давления-объём-энергия продуктов детонации взрывчатых веществ в приложениях связанных с ускорением твердых тел. Значения действительны только для больших расходов.
 
Уравнением состоянием было выбрано уравнение Джонсона-Вилкинса-Ли (Jones-Wilkins-Lee). Используется для точного описания поведения давления-объём-энергия продуктов детонации взрывчатых веществ в приложениях связанных с ускорением твердых тел. Значения действительны только для больших расходов.
 
::<math>
 
::<math>
−
P = A(1-ω/(R1V))e^(-R1V) + B(1-ω/(R2V))e^(-R2V) + ωE/V
+
P = A(1-\frac{ω}{R_1V}))e^{-R_1V} + B(1-\frac{ω}{R_2V})e^{-R_2V} + \frac{ωE}{V}
 
</math>
 
</math>
 
где A и B -линейные коэффициенты [Па]; R1, R2, ω - нелинейные коэффициенты [безразмерные]; P - давление [Па]; E - энергия [Па-м^3/v^3]
 
где A и B -линейные коэффициенты [Па]; R1, R2, ω - нелинейные коэффициенты [безразмерные]; P - давление [Па]; E - энергия [Па-м^3/v^3]
Строка 46: Строка 46:
 
{| class="wikitable"
 
{| class="wikitable"
 
|-
 
|-
−
! A !! B !! R1 !! R2 !! ω !! E0 !! ρ !! υ
+
! A !! B !! R_1 !! R_2 !! ω !! E_0 !! ρ !! υ
 
|-
 
|-
 
| 8,364e11 || 1,298e10 || 4,62 || 1,25 || 0,42 || 9,5e9 || 1865 || 8470
 
| 8,364e11 || 1,298e10 || 4,62 || 1,25 || 0,42 || 9,5e9 || 1865 || 8470
Строка 54: Строка 54:
  
 
Расчёт проводится в решателе LS-DYNA, многоцелевом конечно-элементный комплексе, предназначенный для анализа высоконелинейных и быстротекущих процессов в задачах механики твердого и жидкого тела. LS-DYNA представляет возможность эффективного численного моделирования высоконелинейных термомеханических процессов.  
 
Расчёт проводится в решателе LS-DYNA, многоцелевом конечно-элементный комплексе, предназначенный для анализа высоконелинейных и быстротекущих процессов в задачах механики твердого и жидкого тела. LS-DYNA представляет возможность эффективного численного моделирования высоконелинейных термомеханических процессов.  
 +
 +
 +
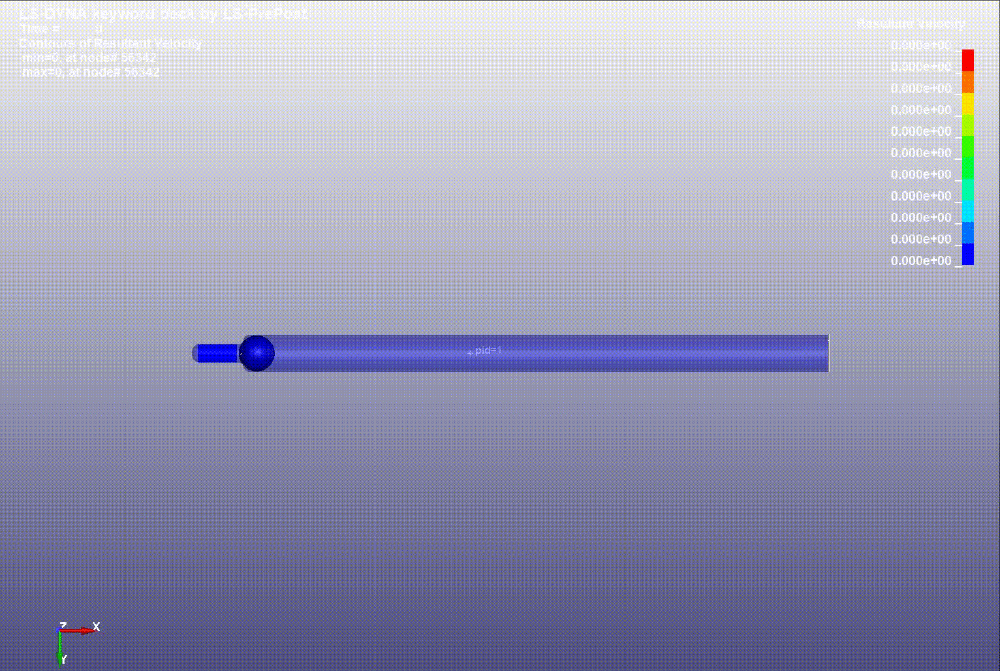
[[File:Movie 000.gif|1000px|Анимация выстрела|]]
 +
 +
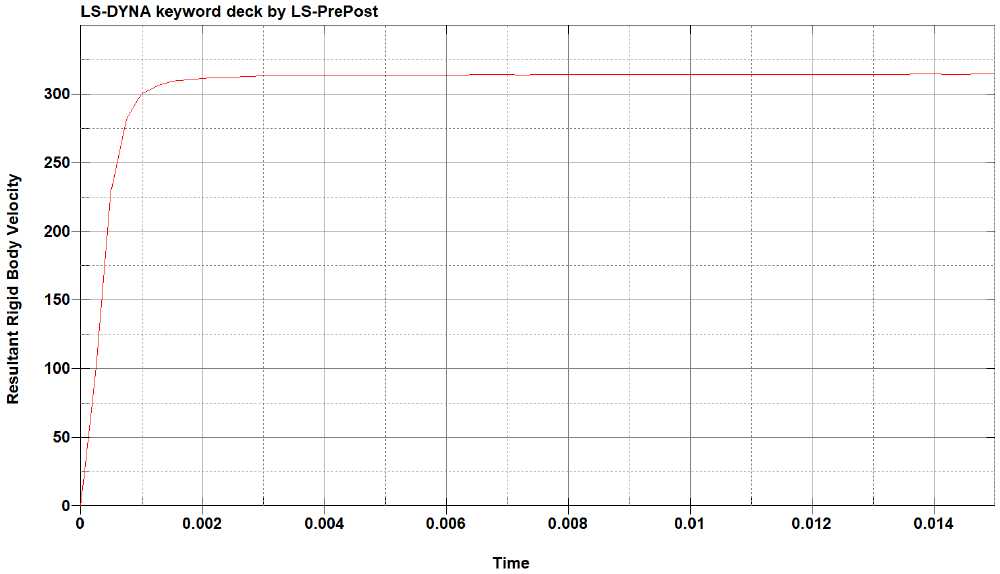
[[File:Velosity.png|1000px|График скорости ядра от времени]]
  
 
== Результаты ==
 
== Результаты ==
Строка 59: Строка 64:
 
* В задаче происходят вылеты частиц через поверхность орудия, их процент мал по отношению к количеству частиц оставшихся в области ствола, однако это тоже влияет на решение, поскольку вылетают те частицы, у которых скорость наибольшая. Возможными вариантами решения могут являться: уменьшение размера сетки и более точная настройка контакта частицы-стенки. Дальнейшее уменьшение размера шага по времени не уменьшило количество вылетающих частиц.
 
* В задаче происходят вылеты частиц через поверхность орудия, их процент мал по отношению к количеству частиц оставшихся в области ствола, однако это тоже влияет на решение, поскольку вылетают те частицы, у которых скорость наибольшая. Возможными вариантами решения могут являться: уменьшение размера сетки и более точная настройка контакта частицы-стенки. Дальнейшее уменьшение размера шага по времени не уменьшило количество вылетающих частиц.
 
* Скорее всего для данной задачи ALE постановка давала бы более точные решения при тех же затратах, поскольку контакт с границами можно было задать более точно и вылетов за пределы орудия в ALE постановке не было бы.
 
* Скорее всего для данной задачи ALE постановка давала бы более точные решения при тех же затратах, поскольку контакт с границами можно было задать более точно и вылетов за пределы орудия в ALE постановке не было бы.
−
* Скорость ядра в момент вылета из пушки составляет порядка 280 м/с, что соответствует реальным данным.
+
* Скорость ядра в момент вылета из пушки составляет порядка 315 м/с, что соответствует реальным данным.
  
 
== Список источников ==
 
== Список источников ==

Версия 16:37, 5 апреля 2019

Курсовые работы 2018-2019 учебного года > Моделирование взрыва в SPH постановке

Курсовой проект по Механике дискретных сред

Исполнитель: Уманский Александр

Группа: 43604/1

Семестр: осень 2018

Постановка задачи

Gun.jpg

Дана геометрия реальной осадной пищали 17 века. Упростить геометрию задачи, провести моделирование взрыва пороха в стволе орудия, найти скорость вылета ядра.

Упрощение геометрии

Фактически для моделирования взрыва и нахождения скорости снаряда на вылете из орудия необходимы: ядро, рабочая часть орудия (внутренняя его часть) и порох. При этом, чтобы упростить задачу, было решено моделировать ядро и орудие абсолютно жёсткими. Тогда поскольку для абсолютно жёсткого тела в нашей задаче толщина орудия не имеет значения (от неё будет изменяться только вес) оно моделируется с помощью поверхности. Ядро было оставлено твёрдым телом, с пустой полостью внутри. Блок с порохом будет генерироваться позднее.

Исходная геометрия
Геометрия после упрощения

Подготовка модели и допущения

Подготовка модели производилась в 2-х програмных пакетах Ansys ls-dyna и ls-prepost 4.6, возможно было подготовить модель полностью в LS-prepost, однако ansys позволяет сильно сократить время подготовки.

Упрощения:

  • В задаче трение между орудием и снарядом пренебрегаем, это связано со сложностью данного контакта в реальности (трение будет существенно нелинейным в связи с тем что при выстреле между ядром и орудием возникают газовые прослойки, однако они не равномерны) и тем что значение сил трения будет малыми по сравнению с силами выталкивающими снаряд.
  • Поскольку трением мы пренебрегли скажем, что снаряд может двигаться только вдоль оси орудия, по остальным осям, а так же его повороты будем считать равными нулю.

Для моделирования взрыва в численных пакетах используются 2 основных постановки: ALE-постановка и SPH-постановка.

В ALE постановке последовательно итерируются формулировка Лагранжа, когда сетка КЭ и материал жестко связаны и могут двигаться только совместно и формулировка Эйлера, когда сетка КЭ является неподвижной и абсолютно жёсткой, а материал может перемещаться между элементами. ALE более распространена для данного типа задач и лучше подходит для задач, где взрыв происходит в ограниченной области.

Для взрывов в открытом пространстве удобнее использовать бессеточные методы такие как SPH, поскольку в данных задачах происходит сильное искажение сетки, что может привести к большим ошибкам или высоким затратам на вычисления. Метод гидродинамики сглаженных частиц является бессеточным лагранжевым методом (то есть координаты движутся вместе с жидкостью), т.е. метод разбивает тело на дискретные элементы, называемые частицами. Плюсами метода являются простая численная реализация и простая связь с механикой сплошной среды. Минусом являются численные артефакты.

Уравнением состоянием было выбрано уравнение Джонсона-Вилкинса-Ли (Jones-Wilkins-Lee). Используется для точного описания поведения давления-объём-энергия продуктов детонации взрывчатых веществ в приложениях связанных с ускорением твердых тел. Значения действительны только для больших расходов.

[math] P = A(1-\frac{ω}{R_1V}))e^{-R_1V} + B(1-\frac{ω}{R_2V})e^{-R_2V} + \frac{ωE}{V} [/math]

где A и B -линейные коэффициенты [Па]; R1, R2, ω - нелинейные коэффициенты [безразмерные]; P - давление [Па]; E - энергия [Па-м^3/v^3]


В качестве взрывчатого материала была выбрана модификация пороха LX-04-1 с параметрами приведёнными в таблице ниже. Создаем

A B R_1 R_2 ω E_0 ρ υ
8,364e11 1,298e10 4,62 1,25 0,42 9,5e9 1865 8470

Решение

Расчёт проводится в решателе LS-DYNA, многоцелевом конечно-элементный комплексе, предназначенный для анализа высоконелинейных и быстротекущих процессов в задачах механики твердого и жидкого тела. LS-DYNA представляет возможность эффективного численного моделирования высоконелинейных термомеханических процессов.


Movie 000.gif

График скорости ядра от времени

Результаты

  • В результате моделирования была получена модель орудия, описывающая процесс с момента начала детонации до момента вылета ядра из орудия.
  • В задаче происходят вылеты частиц через поверхность орудия, их процент мал по отношению к количеству частиц оставшихся в области ствола, однако это тоже влияет на решение, поскольку вылетают те частицы, у которых скорость наибольшая. Возможными вариантами решения могут являться: уменьшение размера сетки и более точная настройка контакта частицы-стенки. Дальнейшее уменьшение размера шага по времени не уменьшило количество вылетающих частиц.
  • Скорее всего для данной задачи ALE постановка давала бы более точные решения при тех же затратах, поскольку контакт с границами можно было задать более точно и вылетов за пределы орудия в ALE постановке не было бы.
  • Скорость ядра в момент вылета из пушки составляет порядка 315 м/с, что соответствует реальным данным.

Список источников

Источник — «http://tm.spbstu.ru/?title=Моделирование_взрыва_в_SPH_постановке&oldid=52967»