Моделирование взрыва в SPH постановке — различия между версиями

Материал из Department of Theoretical and Applied Mechanics
Перейти к: навигация, поиск
м
(→‎Подготовка модели и допущения)
Строка 29: Строка 29:
 
*Поскольку трением мы пренебрегли скажем, что снаряд может двигаться только вдоль оси орудия, по остальным осям, а так же его повороты будем считать равными нулю.
 
*Поскольку трением мы пренебрегли скажем, что снаряд может двигаться только вдоль оси орудия, по остальным осям, а так же его повороты будем считать равными нулю.
  
−
Для моделирования взрыва в численных пакетах используются 2 основных постановки: ALE-постановка и SPH-постановка. В ALE постановке последовательно итерируются постановка Лагранжа
+
Для моделирования взрыва в численных пакетах используются 2 основных постановки: ALE-постановка и SPH-постановка.  
  
 +
В ALE постановке последовательно итерируются формулировка Лагранжа, когда сетка КЭ и материал жестко связаны и могут двигаться только совместно и формулировка Эйлера, когда сетка КЭ является неподвижной и абсолютно жёсткой, а материал может перемещаться между элементами. ALE более распространена для данного типа задач и лучше подходит для задач, где взрыв происходит в ограниченной области.
 +
 +
Для взрывов в открытом пространстве удобнее использовать бессеточные методы такие как SPH, поскольку в данных задачах происходит сильное искажение сетки, что может привести к большим ошибкам или высоким затратам на вычисления. Метод гидродинамики сглаженных частиц является бессеточным лагранжевым методом (то есть координаты движутся вместе с жидкостью), т.е. метод разбивает тело на дискретные элементы, называемые частицами. Плюсами метода являются простая численная реализация и простая связь с механикой сплошной среды. Минусом являются численные артефакты.
  
 
== Решение ==
 
== Решение ==

Версия 01:48, 5 апреля 2019

Курсовые работы 2018-2019 учебного года > Моделирование взрыва в SPH постановке

Курсовой проект по Механике дискретных сред

Исполнитель: Уманский Александр

Группа: 43604/1

Семестр: осень 2018

Постановка задачи

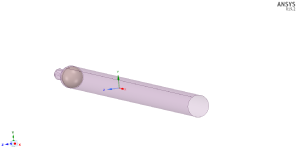
Дана геометрия реальной осадной пищали 17 века. Упростить геометрию задачи, провести моделирование взрыва пороха в стволе орудия, найти скорость вылета ядра.

Упрощение геометрии

Фактически для моделирования взрыва и нахождения скорости снаряда на вылете из орудия необходимы: ядро, рабочая часть орудия (внутренняя его часть) и порох. При этом, чтобы упростить задачу, было решено моделировать ядро и орудие абсолютно жёсткими. Тогда поскольку для абсолютно жёсткого тела в нашей задаче толщина орудия не имеет значения (от неё будет изменяться только вес) оно моделируется с помощью поверхности.

Geom2.png
Geom1.png

Подготовка модели и допущения

Подготовка модели производилась в 2-х програмных пакетах Ansys ls-dyna и ls-prepost 4.6, возможно было подготовить модель полностью в LS-prepost, однако ansys позволяет сильно сократить время подготовки.

Упрощения:

  • В задаче трение между орудием и снарядом пренебрегаем, это связано со сложностью данного контакта в реальности (трение будет существенно нелинейным в связи с тем что при выстреле между ядром и орудием возникают газовые прослойки, однако они не равномерны) и тем что значение сил трения будет малыми по сравнению с силами выталкивающими снаряд.
  • Поскольку трением мы пренебрегли скажем, что снаряд может двигаться только вдоль оси орудия, по остальным осям, а так же его повороты будем считать равными нулю.

Для моделирования взрыва в численных пакетах используются 2 основных постановки: ALE-постановка и SPH-постановка.

В ALE постановке последовательно итерируются формулировка Лагранжа, когда сетка КЭ и материал жестко связаны и могут двигаться только совместно и формулировка Эйлера, когда сетка КЭ является неподвижной и абсолютно жёсткой, а материал может перемещаться между элементами. ALE более распространена для данного типа задач и лучше подходит для задач, где взрыв происходит в ограниченной области.

Для взрывов в открытом пространстве удобнее использовать бессеточные методы такие как SPH, поскольку в данных задачах происходит сильное искажение сетки, что может привести к большим ошибкам или высоким затратам на вычисления. Метод гидродинамики сглаженных частиц является бессеточным лагранжевым методом (то есть координаты движутся вместе с жидкостью), т.е. метод разбивает тело на дискретные элементы, называемые частицами. Плюсами метода являются простая численная реализация и простая связь с механикой сплошной среды. Минусом являются численные артефакты.

Решение

Расчёт проводится в решателе LS-DYNA, многоцелевом конечно-элементный комплексе, предназначенный для анализа высоконелинейных и быстротекущих процессов в задачах механики твердого и жидкого тела. LS-DYNA представляет возможность эффективного численного моделирования высоконелинейных термомеханических процессов.

Список источников

Источник — «http://tm.spbstu.ru/?title=Моделирование_взрыва_в_SPH_постановке&oldid=52960»