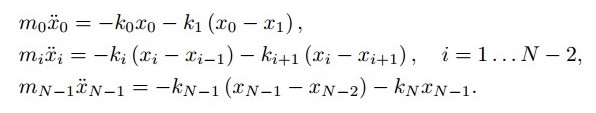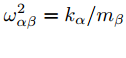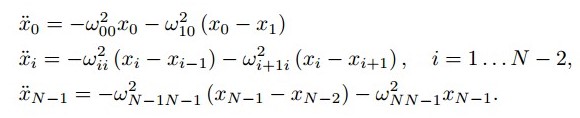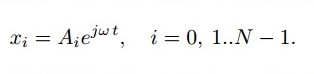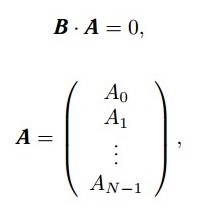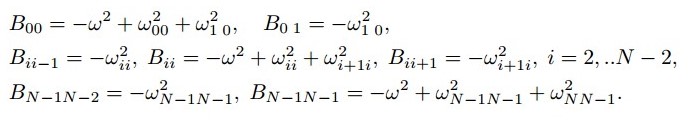Моделирование вынужденных колебаний цепочки связанных гармонических осцилляторов — различия между версиями
| Строка 1: | Строка 1: | ||
| − | [[ Курсовые_работы_по_ВМДС:_2018-2019 | Курсовые работы 2018-2019 учебного года]] > '''Моделирование | + | [[ Курсовые_работы_по_ВМДС:_2018-2019 | Курсовые работы 2018-2019 учебного года]] > '''Моделирование свободных колебаний цепочки связанных гармонических осцилляторов''' <HR> |
'''''Курсовой проект по [[Механика дискретных сред|Механике дискретных сред]]''''' | '''''Курсовой проект по [[Механика дискретных сред|Механике дискретных сред]]''''' | ||
| Строка 11: | Строка 11: | ||
===Постановка задачи=== | ===Постановка задачи=== | ||
| − | Рассмотрим движения движение цепочки связанных гармонических осцилляторов | + | Рассмотрим движения движение цепочки связанных гармонических осцилляторов - модель, представляющая собой систему шариков с массами m, cвязанных между собой пружинками одинаковой жесткости k. |
| + | |||
[[File:1dfgs.jpg|center]] | [[File:1dfgs.jpg|center]] | ||
===Решение=== | ===Решение=== | ||
| − | + | Запишем уравнения движения для каждой массы колебательной системы (1): | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[File:1 1.jpg|center]] | |
| − | + | Для удобства дальнейшего решения запишем уравнение (1), введя обозначение | |
| − | [[File: | + | [[File:1 12.png|center]] |
| − | + | в следующем виде (2): | |
| − | 1 | + | [[File:2 1.jpg|center]] |
| − | + | Ищем решение системы дифференциальных уравнений в виде (3): | |
| − | 3 | + | [[File:3 1.jpg|center]] |
| − | 4) | + | Подставив (3) в систему (2), сгруппировав члены, и записав систему в матричном виде, получим (4): |
| − | + | [[File:4 1.jpg|center]] | |
| − | + | B - трехдиагональная матрица, элементы которой вычисляются по следующим правилам (5): | |
| − | + | [[File:5 1.jpg|center]] | |
| − | + | Алгоритм решения данной задачи реализуется в MATLAB. | |
| − | + | Результат работы можно посмотреть на графике зависимости значений смещений тел от времени: | |
| − | [[File: | + | [[File:M=1,k=5,R1=0.5,N=50.gif|center]] |
== См. также == | == См. также == | ||
Версия 21:10, 26 января 2019
Курсовые работы 2018-2019 учебного года > Моделирование свободных колебаний цепочки связанных гармонических осцилляторовКурсовой проект по Механике дискретных сред
Исполнитель: Васильева Анастасия
Группа: 43604/1
Семестр: осень 2018
Постановка задачи
Рассмотрим движения движение цепочки связанных гармонических осцилляторов - модель, представляющая собой систему шариков с массами m, cвязанных между собой пружинками одинаковой жесткости k.
Решение
Запишем уравнения движения для каждой массы колебательной системы (1):
Для удобства дальнейшего решения запишем уравнение (1), введя обозначение
в следующем виде (2):
Ищем решение системы дифференциальных уравнений в виде (3):
Подставив (3) в систему (2), сгруппировав члены, и записав систему в матричном виде, получим (4):
B - трехдиагональная матрица, элементы которой вычисляются по следующим правилам (5):
Алгоритм решения данной задачи реализуется в MATLAB.
Результат работы можно посмотреть на графике зависимости значений смещений тел от времени: