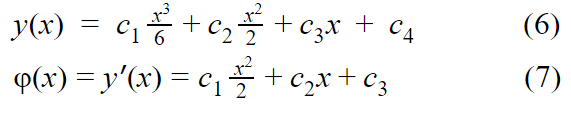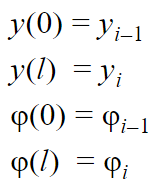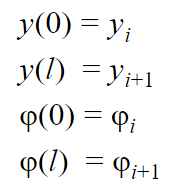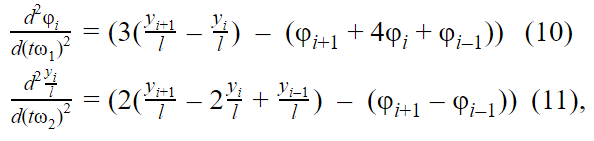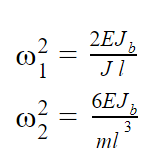Перераспределение энергии между поступательными и вращательными степенями свободы — различия между версиями
Anpolol (обсуждение | вклад) (→Вывод уравнений) |
Anpolol (обсуждение | вклад) (→Вывод уравнений) |
||
| Строка 8: | Строка 8: | ||
Все тела соединены стержнями, которые описываются уравнением балки Бернулли - Эйлера. | Все тела соединены стержнями, которые описываются уравнением балки Бернулли - Эйлера. | ||
Движение каждого тела - точки описывается уравнениями: | Движение каждого тела - точки описывается уравнениями: | ||
| − | [[File:Уранвения1. | + | [[File:Уранвения1.png]] <br /> |
Моменты и силы находим по определению: | Моменты и силы находим по определению: | ||
| Строка 16: | Строка 16: | ||
Вид функции y(x) найдем из уравнения Балки - Бернулли Эйлера: | Вид функции y(x) найдем из уравнения Балки - Бернулли Эйлера: | ||
| − | [[File: | + | [[File:Уранвения33.png]] <br /> |
получаем: | получаем: | ||
| − | [[File: | + | [[File:Уранвения4.png]] <br /> |
Для поиска коэффициентов необходимы граничные условия. | Для поиска коэффициентов необходимы граничные условия. | ||
| Строка 38: | Строка 38: | ||
Перепишем уравнения в виде: | Перепишем уравнения в виде: | ||
| − | [[File: | + | [[File:Уранвения66.png]] <br /> |
| + | |||
где | где | ||
[[File:Где.png]] <br /> | [[File:Где.png]] <br /> | ||
Получили обезразмеренные уравнения: | Получили обезразмеренные уравнения: | ||
| − | [[File: | + | [[File:Уранвения7.png]] <br /> |
Теперь можно переходить к численному интегрированию. | Теперь можно переходить к численному интегрированию. | ||
Версия 01:06, 24 декабря 2018
Постановка задачи
Рассмотреть перераспределение энергии между вращательными и поступательными степенями свободы в системе из N тел-точек, соединенных друг с другом балками Бернулли-Эйлера.
Вывод уравнений
Рассматривается система из N тел-точек. Каждое тело имеет две степени свободы - смещение вдоль вертикальной оси yi, и угол поворота относительно вертикальной оси i.
Все тела соединены стержнями, которые описываются уравнением балки Бернулли - Эйлера.
Движение каждого тела - точки описывается уравнениями:
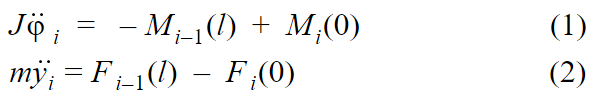
Моменты и силы находим по определению:
Движение каждого тела - точки описывается уравнениями:
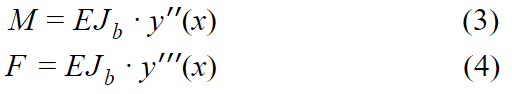
Вид функции y(x) найдем из уравнения Балки - Бернулли Эйлера:
получаем:
Для поиска коэффициентов необходимы граничные условия. На участке соединяющим i-1 и i тела :
и на участке, соединяющим i и i+1 тела-точки:
где l- длина балки.
Учитывая граничные условия, приведенные выше, и формулы (1-7) находим уравнения движения i-го тела:
Файл:Уравнения55.png
Получили обезразмеренные уравнения:
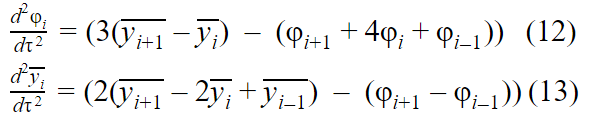
Теперь можно переходить к численному интегрированию.