Мещерский 48.41 — различия между версиями

Версия 00:28, 22 декабря 2017

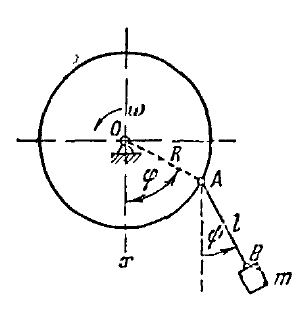
Задача 48.41 из сборника задач Мещерского Задача:Смоделировать движение системы из диска и маятника, прикрепленного к нему(см рис.) на языке программирования JS .

Маятник на Диске

Решение: Задачу решаем для малых колебаний. Углы отклонения диска и маятника от вертикали соответственно [math]\varphi [/math] и [math]\psi [/math]. Радиус диска и длина нити соответственно R и l, Их массы M и m. Момент инерции диска [math]I=\frac{MR^2}{2}[/math].

Так как углы отклонения небольшие, то можно считать, что к диску в точке крепления нити приложена постоянная, вертикально направленная вниз сила тяжести(вес) маятника [math] P=mg[/math]. Тогда уравнение движения диска принимает вид уравнения движения физического маятника:

По 2-му закону Ньютона для вращательного движения [math]M=Iβ=I \ddot \varphi [/math].

[math] M=-Rmgsin\varphi=-Rmg\varphi=I\ddot\varphi [/math]

Таким образом,

[math]\ddot\varphi+\frac{2mg}{MR}\varphi=0[/math]

Аналгочино получаем уравнение для маятника:

[math]\ddot\psi+\frac{g}{l}\psi=0[/math]

Реализация при помощи JS