Преобразование механической энергии в тепловую в одномерном кристалле — различия между версиями

Версия 15:42, 13 августа 2017

Выпускная квалификационная работа

Выполнил: студент группы 43604/1 Е. Б. Старобинский

Руководитель: доктор физ.-мат. наук, член-корр. РАН А. М. Кривцов

Введение

Cовременные нанотехнологии позволяют получать практически идеальные (бездефектные) материалы^[1][2], отличающиеся по своим свойствам от материалов с дефектами^[3]. В частности, тепловые процессы в таких наноструктурах протекают по иным, более сложным законам, чем для тел макроуровня. Знание этих законов и особенностей поведения наносистем имеет большое практическое значение при разработке новых устройств^[4][5] и расширении области применения наноматериалов, в том числе на промышленном уровне. Однако описание наносистем с помощью существующих моделей сопряжено с существенными противоречиями экспериментальным данным, что связано как с отсутствием цельной теории, позволяющей описывать процессы наноуровня, так и с трудоёмкостью проведения натурных экспериментов. Компромиссом является численное моделирование наноструктур, при котором поведение материала является прямым следствием уравнений динамики. Минус такого подхода – необходимость рассчитывать крупные фрагменты материала, чтобы за исследумое время возмущение не успевало дойти до границ. Следовательно, требуются большие вычислительные мощности.

В 1953 году на суперкомпьютере Maniac I группа учёных, состоящая из Энрико Ферми, Станислава Улама, Джона Паста и Мэри Цингоу, численно решила задачу Коши^[6] для системы дифференциальных уравнений, описывающую одномерный кристалл с нелинейным взаимодействием между частицами. С помощью синусоидальной волны задавалось начальное возмущение, ожидалось, что с течением времени энергия волны равномерно распределится по всем частицам. Оказалось, что сначала волна действительно теряет свою форму и энергию, но по прошествии достаточного времени почти точно возвращается к исходному состоянию. В дальнейшем это явление было названо «парадоксом Ферми-Паста-Улама-Цингоу», так как исследователям удалось доказать неспособность физики 20-го века описывать взаимодействия на наноуровне.

В данной работе рассматривается одна из нелинейных моделей кристалла, описанных Энрико Ферми. Ключевым отличием является введение тепловой энергии через задание дисперсии начальных скоростей.

Модель одномерного кристалла

Метод исследования

Объектом исследования является модель одномерного теплоизолированного кристалла с заданной на нём механической волной. Начальная температура кристалла задаётся случайными скоростями частиц. Дифференциальные уравнения динамики цепочки решаются методом центральных разностей. Производится сравнение решений для бегущей и стоячей волн. Исследуется закон перехода механической энергии волны в тепловую энергию кристалла.

Для численного расчета формулируемых задач создан ряд специальных программ на языках С++, Bash и Mathematica.

Постановка задачи

Рассмотрим модель одномерного кристалла: цепочку одинаковых частиц массы [math]m[/math], соединённых одинаковыми нелинейными пружинами (квадратичная нелинейность).

Каждой частице присвоим свой целочисленный индекс. Принимая [math]u_k[/math] за перемещение [math]k[/math]-й частицы, а [math]C_1[/math] и [math]C_2[/math] — за коэффициенты при линейном и квадратичном членах в разложении силы взаимодействия [math]k[/math]-й частицы с двумя ближайшими соседями, получим следующее дифференциальное уравнение:

[math] \begin{equation} m\ddot u_k = C_1\left(\left(u_{k + 1} - u_{k}\right) - \left(u_{k} - u_{k - 1}\right)\right) + C_2\left(\left(u_{k + 1} - u_{k}\right)^2 - \left(u_{k} - u_{k - 1}\right)^2\right), \end{equation} [/math]

где [math]\dot f[/math] — производная [math]f[/math] по времени

Перепишем это выражение, раскрыв скобки и введя новые обозначения для коэффициентов при линейной и нелинейной части:

[math] \begin{equation} \ddot u_k = \omega_0^2\left(u_{k + 1} - 2u_{k} + u_{k - 1}\right) + \alpha_0^2\left(u_{k + 1}^2 - 2u_{k + 1}u_{k} + 2u_{k}u_{k - 1} - u_{k - 1}^2\right), \end{equation} [/math]

[math] \begin{equation} \omega_0 = \sqrt{\frac{C_1}{m}}, \quad \alpha_0 = \sqrt{\frac{C_2}{m}}. \end{equation} [/math]

Здесь [math]\omega_0[/math] соответствует циклической частоте колебаний.

Заметим, что

[math] \begin{equation} \begin{split} & u_{k + 1}^2 - 2u_{k + 1}u_{k} + 2u_{k}u_{k - 1} - u_{k - 1}^2 = \\ & = u_{k + 1}^2 - 2u_{k + 1}u_{k} + 2u_{k}u_{k - 1} - u_{k - 1}^2 \pm u_{k + 1}u_{k-1}= \\ & = \left(u_{k + 1}^2 - 2u_{k + 1}u_{k} + u_{k - 1}u_{k + 1}\right) - \left(u_{k + 1}u_{k - 1} - 2u_{k}u_{k - 1} + u_{k - 1}^2\right) = \\ & = u_{k + 1}\left(u_{k + 1} - 2u_{k} + u_{k - 1}\right) - u_{k - 1}\left(u_{k + 1} - 2u_{k} + u_{k - 1}\right) = \\ & = \left(u_{k + 1} - 2u_{k} + u_{k - 1}\right)\left( u_{k + 1} - u_{k - 1} \right). \end{split} \label{replace} \end{equation} [/math]

Воспользуемся этой заменой, и тогда уравнения динамики цепочки примут следующий вид:

[math] \begin{equation} \ddot u_k = \left(u_{k + 1} - 2u_{k} + u_{k - 1} \right) \left( \omega_0^2 + \alpha_0^2 \left( u_{k + 1} - u_{k - 1} \right) \right). \label{chainEquations} \end{equation} [/math]

Аналогичное уравнение использовалось в оригинальной работе Ферми, Паста и Улама^[6].

Механическую энергию системы в начальный момент времени (то есть, при [math]t = 0[/math]) будем задавать с помощью синусоидальной волны. Из-за теплового движения частиц волна будет терять свою форму, а её энергия перейдёт в тепловую энергию системы. Для описания этого процесса численно решим уравнения динамики кристалла.

Чтобы замкнуть систему из [math]k[/math] уравнений динамики, определим граничные условия, а также по [math]k[/math] начальных условий на перемещения и скорости. Для задания начальных скоростей воспользуемся генератором случайных чисел с равномерным распределением. При этом дисперсию скоростей будем задавать в соответствии с требуемым температурным профилем.

Начальные и граничные условия

Чтобы соответствовать идеальной модели, исследуемая цепочка должна иметь бесконечную длину. Для проведения численного моделирования будем рассматривать кристалл конечной длины с заданным условием периодичности (граничные условия Борна-Кармана):

[math] \begin{equation} \label{boundaryConditions} u\!\left(x + L\right) = u\!\left(x\right), \quad L \gg a, \end{equation} [/math]

где [math]L[/math] — длина кристалла, [math]a[/math] — равновесное расстояние между частицами.

Таким образом, условие теплоизоляции выполняется.

В рамках поставленной задачи будем рассматривать два вида движения в кристалле: движение механической волны и тепловое движение (тепловой шум). Соответственно, начальные условия для скоростей частиц также будут складываться из двух компонент. Меняя начальные условия, рассмотрим решение задачи для следующих постановок:

• на кристалле задана бегущая волна;
• на кристалле задана стоячая волна.

Начальные условия для бегущей волны

Рассмотрим уравнение бегущей волны (пусть волна распространяется в одном направлении):

[math] \begin{equation} \label{runningWaveEquation1} \dot u\!\left(x\right) = A \sin\!\left(k_0 x - \omega_0 t + \phi \right), \end{equation} [/math]

где [math]A[/math] — амплитуда колебаний, [math]k_0[/math] — волновое число, [math]\phi[/math] — фаза колебаний.

Величину [math]u\!\left(x\right)[/math] на момент времени [math]t[/math] получим интегрированием уравнения волны:

[math] \begin{equation} \label{runningWaveEquation2} u\!\left(x\right) = \int\limits_0^t \! \dot u\!\left(x\right) \,\mathrm{d}t = \frac{1}{\omega_0} A \cos\!\left(k_0 x - \omega_0 t + \phi \right). \end{equation} [/math]

Пусть длина волны совпадает с длиной кристалла, тогда

[math] \begin{equation} k_0~\mathrel{\stackrel{\rm def}=} \frac{2 \pi}{\lambda} = \frac{2 \pi}{L}, \end{equation} [/math]

где [math]\lambda[/math] — длина волны.

Фазу колебаний [math]\phi[/math] положим равной нулю и запишем уравнения для [math]u[/math] и [math]\dot u[/math] для начального момента времени ([math]t=0[/math]):

[math] \begin{equation} \label{initialMechanicalVelocity1} \dot u\!\left(x\right)|_{t=0} = A \sin\!\left(\frac{2 \pi x}{L} \right). \end{equation} [/math]

[math] \begin{equation} \label{initialMechanicalDisplacement1} u\!\left(x\right)|_{t=0} = \frac{1}{\omega_0} A \cos\!\left(\frac{2 \pi x}{L}\right). \end{equation} [/math]

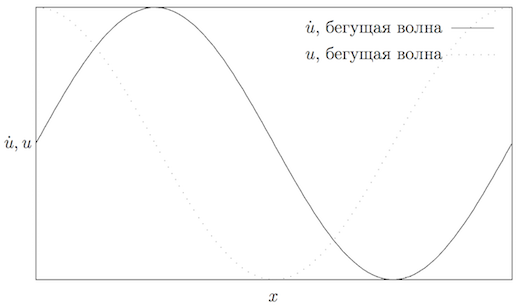
На рисунке 1 приведён график начальных перемещений и скоростей частиц кристалла при заданной бегущей волне.

Рисунок 1. Начальные условия для бегущей волны

Начальные условия для стоячей волны

Начальные условия, описанные в предыдущем пункте, позволяют задать бегущую волну. Получим подобные условия также для стоячей волны. Для этого рассмотрим две волны амплитуды [math]\frac{A}{2}[/math], бегущие в противоположных направлениях с разностью фаз [math]\pi[/math]:

[math] \begin{equation} v_1\!\left(x\right) = \frac{A}{2} \sin\!\left(k_0 x - \omega_0 t \right), \quad v_2\!\left(x\right) = \frac{A}{2} \sin\!\left(- k_0 x - \omega_0 t + \pi \right), \end{equation} [/math]

Результатом наложения этих двух волн будет стоячая волна, описываемая следующим уравнением:

[math] \begin{equation} \label{standingWaveEquation1} \dot u\!\left(x\right) = v_1\!\left(x\right) + v_1\!\left(x\right) = A \cos\!\left(\omega_0 t \right)\sin\left(k_0 x \right). \end{equation} [/math]

Аналогично, проинтегрируем это уравнение по времени [math]t[/math]:

[math] \begin{equation} u\!\left(x\right) = \int\limits_0^t \! \dot u\!\left(x\right) \,\mathrm{d}t = \frac{A}{\omega_0} \sin\!\left(\omega_0 t \right)\sin\left(k_0 x \right). \label{standingWaveEquation2} \end{equation} [/math]

Подставляя в уравнения для [math]u[/math] и [math]\dot u[/math] [math]k_0 = \frac{2 \pi}{L}[/math] и [math]t = 0[/math], получим начальные условия для стоячей волны:

[math] \begin{equation} \label{initialMechanicalVelocity2} \dot u\!\left(x\right)|_{t=0} = A \sin\!\left(\frac{2 \pi x}{L} \right). \end{equation} [/math]

[math] \begin{equation} \label{initialMechanicalDisplacement2} u\!\left(x\right)|_{t=0} = 0. \end{equation} [/math]

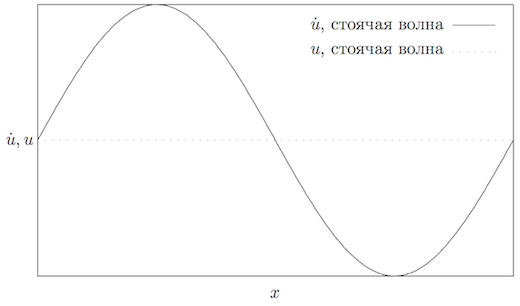
Соответствующий график начальных перемещений и скоростей частиц цепочки приведён на рисунке 2.

Рисунок 2. Начальные условия для стоячей волны

Функции скоростей в начальный момент времени для бегущей и стоячей волн совпадают, различаются только начальные перемещения.

Начальные условия теплового движения

Введём оператор усреднения функции по её аргументу:

[math] \begin{equation} \left\lt f\right\gt = \frac{1}{b - a}\int\limits_{a}^{b} \! f \! \left( x \right) \, \mathrm{d}x, \end{equation} [/math]

где [math]\left[a; b\right][/math] — отрезок, на котором проводится усреднение.

Оператор нахождения среднего по координате для цепочки длины [math]L[/math] в таком случае записывается следующим образом:

[math] \begin{equation} \left\lt f\right\gt = \frac{1}{L}\int\limits_{0}^{L} \! f \! \left( x \right) \, \mathrm{d}x, \end{equation} [/math]

Чтобы получить выражение для тепловой компоненты скорости, запишем определение кинетической температуры в одномерной постановке:

[math] \begin{equation} \frac{1}{2}kT\!\left(x\right) = \frac{m \left\lt v^{2} \right\gt }{2}, \end{equation} [/math]

где [math]k[/math] — постоянная Больцмана, [math]T(x)[/math] — профиль температуры, [math]v[/math] — скорость.

Из этого равенства выразим [math]\left\lt v^{2} \right\gt [/math]:

[math] \begin{equation} \left\lt v^{2} \right\gt = \frac{kT\!\left(x\right)}{m}. \label{vTemp2Average} \end{equation} [/math]

Пусть в начальный момент времени температура в кристалле распределена равномерно. Соответствующее распределение для скоростей будем задавать с помощью случайного числа [math]\rho[/math] в диапазоне [math]\left[-1;1\right][/math]. Определим среднее значение [math]\rho^{2}[/math]:

[math] \begin{equation} \left\lt \rho^{2} \right\gt = \frac{1}{2}\int\limits_{-1}^{1} \! \rho^{2} \, \mathrm{d}\rho = \frac{1}{2} \frac{\rho^{3}}{3} \bigg|_{-1}^{1} = \frac{1}{3}. \end{equation} [/math]

Таким образом, [math]3 \left\lt \rho^{2} \right\gt = 1[/math]. Воспользуемся этим соотношением для построения требуемого профиля [math]T \! \left( x \right)[/math]:

[math] \begin{equation} T \! \left( x \right) = 3 \left\lt \rho^{2} \right\gt T_0, \end{equation} [/math]

где [math]T_0[/math] — значение температуры при [math]t = 0[/math].

Перепишем выражение для [math]\left\lt v^{2} \right\gt [/math]:

[math] \begin{equation} \left\lt v^{2} \right\gt = \frac{ 3 k T_0}{m} \left\lt \rho^{2} \right\gt . \end{equation} [/math]

Выразим [math]v^{2}\!\left(x\right)[/math] и [math]v\!\left(x\right)[/math]:

[math] \begin{equation} v^{2}\!\left(x\right) = \frac{ 3 k T_0}{m} \rho^{2}\!\left(x\right), \end{equation} [/math]

[math] \begin{equation} v\!\left(x\right) = \sqrt{\frac{3 k T_0}{m}} \rho\!\left(x\right). \label{vTemp} \end{equation} [/math]

Введём величину дисперсии скоростей [math]\sigma_{v}^{2}[/math] так, чтобы при [math]\sigma_{v}^{2} = 1[/math] в начальный момент времени механическая энергия волны равнялась тепловой энергии цепочки:

[math] \begin{equation} T_0 = \frac{m}{k} A^{2} \sigma_{v}^{2} \label{initialTemp} \end{equation} [/math]

Тогда значение [math]\sigma_{v}^{2} = 10[/math] можно трактовать следующим образом: при [math]t~=~0[/math] энергия теплового шума в кристалле в [math]10[/math] раз превосходит механическую энергию волны.

С учётом этого соотношения получил начальный профиль скоростей:

[math] \begin{equation} v\!\left(x\right)|_{t = 0} = A \sqrt{3 \sigma_{v}^{2}} \rho \! \left( x \right). \label{initialThermalVelocity} \end{equation} [/math]

Таким образом, были получены выражения для обеих компонент скорости: скорость механической волны задаётся синусоидальной функцией, тепловой шум определяется стохастической функцией. Итоговое условие на начальные скорости в кристалле принимает следующий вид:

[math] \begin{equation} \left. \dot u(x) \right |_{t = 0} = A \left( \sin\!\left( \frac{2 \pi x}{L} \right) + \sqrt{3 \sigma_{v}^{2}} \rho \! \left( x \right) \right). \end{equation} [/math]

Начальные перемещения задаются в соответствии с типом рассматриваемой волны.

Вычисление механической энергии

В начальный момент скорость имеет распределение, близкое к синусоидальному. С течением времени цепочка теряет эту форму (в силу нелинейного взаимодействия между частицами), а механическая энергия переходит в тепловую.

Механическая энергия системы [math]E\!\left(x\right)[/math] складывается из кинетической энергии [math]K\!\left(x\right)[/math] и потенциальной энергии [math]\Pi\!\left(x\right)[/math] следующий образом:

[math] \begin{equation} K\!\left( x \right) = \frac{m}{2}\dot u^2\!\left(x\right), \quad \Pi \!\left( x \right) = \frac{C_1}{2}\varepsilon^2\!\left(x\right), \quad E\!\left(x\right) = K\!\left(x\right) + \Pi\!\left(x\right), \label{energyEquations} \end{equation} [/math]

где [math]\varepsilon\!\left(x\right)[/math] — возникающие деформации.

Так как нас интересует энергия не всей системы (включающей тепловой шум), а только заданной механической волны, будем искать энергию первой синусоидальной моды. Перепишем выражения для энергий:

[math] \begin{equation} K\!\left( x \right) = \frac{m}{2}\left(\int\limits_L \! \dot u\!\left(x\right) \sin\!\left( \frac{2 \pi x}{L} \right) \,\mathrm{d}x\right)^2 \end{equation} [/math]

[math] \begin{equation} \Pi \!\left( x \right) = \frac{C_1}{2}\left(\int\limits_L \! \varepsilon\!\left(x\right) \cos\!\left( \frac{2 \pi x}{L} \right) \,\mathrm{d}x\right)^2 \end{equation} [/math]

[math] \begin{equation} E\!\left(x\right) = \frac{m}{2}\left(\int\limits_L \! \dot u\!\left(x\right) \sin\!\left( \frac{2 \pi x}{L} \right) \,\mathrm{d}x\right)^2 + \frac{C_1}{2}\left(\int\limits_L \! \varepsilon\!\left(x\right) \cos\!\left( \frac{2 \pi x}{L} \right) \,\mathrm{d}x\right)^2 \end{equation} [/math]

Первая синусоидальная мода также возникает и в тепловом шуме. Математическое ожидание от её энергии вычислим, усреднив по ансамблю реализаций систему без заданной волны.

Определим значения [math]K\!\left(x\right)[/math] и [math]\Pi\!\left(x\right)[/math] при [math]t = 0[/math]:

[math] \begin{equation} K\!\left( x \right)|_{t=0} = \frac{m}{2}\left(A \int\limits_L \! \sin^2\!\left( \frac{2 \pi x}{L} \right) \,\mathrm{d}x\right)^2, \end{equation} [/math]

[math] \begin{equation} \label{initialPotentialEnergy} \Pi\!\left( x \right)|_{t=0} = \frac{C_1}{2}\left( \int\limits_L \! \varepsilon\!\left(x\right)|_{t = 0} \cos\!\left( \frac{2 \pi x}{L} \right) \,\mathrm{d}x\right)^2 \end{equation} [/math]

Интеграл в формуле (\ref{initialPotentialEnergy}) равен нулю в случае стоячей волны (в начальный момент времени нет деформаций). Покажем, что этот интеграл также будет равен нулю в случае бегущей волны:

[math] \begin{equation} \begin{split} & \int\limits_L \! \varepsilon\!\left(x\right)|_{t = 0} \cos\!\left( \frac{2 \pi x}{L} \right) \,\mathrm{d}x = A \int\limits_L \! \sin\!\left(\frac{2 \pi x}{L}\right) \cos\!\left( \frac{2 \pi x}{L} \right) \,\mathrm{d}x = \\ & = \frac{A}{2} \int\limits_L \! \sin\!\left(\frac{4 \pi x}{L}\right) \,\mathrm{d}x = 0. \end{split} \end{equation} [/math]

То есть, в начальный момент времени потенциальная энергия равна нулю, а механическая энергия задаваемой волны равна

[math] \begin{equation} \label{initialMechanicalEnergy} E\!\left( x \right)|_{t=0} = \frac{m}{2}\left(A \int\limits_L \! \sin^2\!\left( \frac{2 \pi x}{L} \right) \,\mathrm{d}x\right)^2 = \frac{m A^{2} L^{2}}{8} \end{equation} [/math]

Значение (\ref{initialMechanicalEnergy}) выберем в качестве масштаба энергии.

Чтобы определить закон, по которому происходит переход механической энергии в тепловую, введём безразмерный параметр [math]E^*\!\left( x \right) = \frac{E\!\left( x \right)}{E\!\left( x \right)|_{t=0}}[/math] — нормированное значение механической энергии цепочки:

[math] \begin{equation} E^* = \left( \frac{\int\limits_L \! \dot u\!\left(x\right) \sin\!\left( \frac{2 \pi x}{L} \right) \,\mathrm{d}x}{A \int\limits_L \! \sin^2 \left( \frac{2 \pi x}{L} \right) \,\mathrm{d}x} \right)^2 + \omega_0^2 \left( \frac{\int\limits_L \! \varepsilon\!\left(x\right) \cos\!\left( \frac{2 \pi x}{L} \right) \,\mathrm{d}x}{A \int\limits_L \! \sin^2 \left( \frac{2 \pi x}{L} \right) \,\mathrm{d}x} \right)^2. \end{equation} [/math]

Решение задачи свелось к нахождению [math]E^*\!\left( x \right)[/math].

Численное решение дифференциального уравнения

Для решения системы уравнений движения частиц воспользуемся методом центральных разностей. Перепишем граничные условия:

[math] \begin{equation} u_{k + N} = u_{k}, \quad \dot u_{k + N} = \dot u_{k}, \end{equation} [/math]

где [math]N \gg 1[/math] — число независимых частиц.

Вычисление правой части уравнения для [math]\ddot u[/math] аналогично решению с помощью разностной схемы. Рассчитанные таким образом ускорения частиц пересчитываем в скорости:

[math] \begin{equation} \dot u_k\!\left(t + \Delta t\right) = \dot u_k\!\left(t\right) + \ddot u_k\!\left(t\right)\Delta t. \end{equation} [/math]

Затем скорости пересчитываем в смещения частиц. Важно отметить, что по данному методу расчёт скоростей производится на промежуточных шагах по времени относительно расчёта смещений.

[math] \begin{equation} u_k\!\left(t + \Delta t\right) = u_k\!\left(t\right) + \dot u_k\!\left(t\right)\Delta t. \end{equation} [/math]

Значение [math]\varepsilon\!\left(x\right)[/math] вычисляем следующим образом:

[math] \begin{equation} \varepsilon = \sum_{i = 1}^{N - 1} \left(u_{i} - u_{i - 1}\right). \end{equation} [/math]

Параметры расчёта

Для достоверного численного решения дифференциального уравнения относительно [math]\left(u\!\left(x\right), \dot u\!\left(x\right)\right)[/math] длина цепочки должна стремиться к бесконечной, чтобы соответствовать модели идеального кристалла. При проведении численных экспериментов удовлетворительная точность расчётов достигалась на цепочках из 10 миллионов частиц и более.

Статистические характеристики системы также можно вычислить путём усреднения бесконечного множества реализаций (каждая реализация — задача Коши для цепочки). Благодаря этому подходу, предложенному в работа^[7][8], достигается эффективность проводимых численных экспериментов.

Результаты, приводимые далее, получены усреднением [math]5 \cdot 10^4[/math] реализаций цепочки c [math]N = 10^3[/math] (за исключением [math]\rho[/math] все параметры в рамках серии сохранялись). Такая конфигурация будет аналогична модели кристалла с 50 миллионами частиц, но допускает параллельный компьютерный расчёт реализаций. Проведение параллельного моделирования коротких цепочек на суперкомпьютерных системах привело к существенному сокращению общего времени вычислений.

По мере повышения величины дисперсии [math]\sigma_v^2[/math] шаг по времени [math]\Delta t[/math] следует уменьшать. Иначе влияние нелинейной компоненты силы приводит к разрушению системы, эта неустойчивость связана с нарушением условия Куранта. Однако, уменьшение [math]\Delta t[/math] увеличивает время, требуемое для проведения численного моделирования. Так как численно [math]\sigma_v^2[/math] соответствует отношению тепловой энергии в кристалле к энергии механической волны, её значение в реальных системах на несколько порядков превышает исследуемое в рамках данной работы.

В качестве масштаба времени возьмём период колебаний материальной точки массы [math]m[/math] на пружине жёсткости [math]C_1[/math]:

[math] \begin{equation} \quad T_0~\mathrel{\stackrel{\rm def}=} \frac{2 \pi}{\omega_0} = 2 \pi \sqrt{\frac{m}{C_1}}. \end{equation} [/math]

Таблица 1. Параметры при моделировании стоячей волны

Таблица 2. Параметры при моделировании бегущей волны

Значения параметров проводимых экспериментов приведены в таблицах 1 и 2. Моделируемое время ограничено: [math]0 \leq t \leq 7 \cdot 10^4~T_0[/math].

Результаты

Преобразование механической энергии стоячей волны

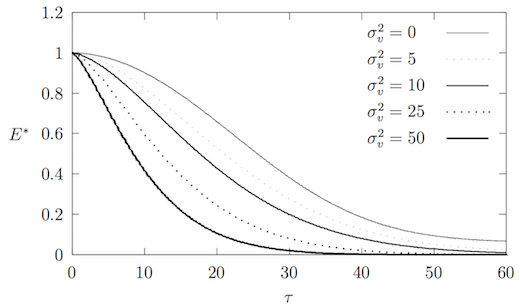
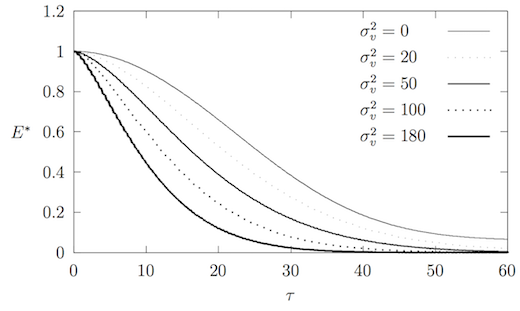
На рисунке 3 приведены вычисленные значения нормированной механической энергии стоячей волны [math]E^*\!\left(\tau\right)[/math] для нескольких значений [math]\sigma_v^2[/math] (здесь и далее [math]\tau = \frac{t}{T_0}[/math] – безразмерное время).

Рисунок 3. Изменение нормированной механической энергии стоячей волны в зависимости от [math]t[/math]

Для одномерного кристалла при отсутствии теплового шума ([math]\sigma_v^2 = 0[/math]) была установлена^[9] следующая зависимость для механической энергии волны:

[math] \begin{equation} E^* \sim e^{-\tau^2}. \label{expectationTau2} \end{equation} [/math]

Подобная зависимость не выполняется при ненулевой дисперсии скоростей частиц цепочки: механическая энергия убывает быстрее при бóльших значениях [math]\sigma_v^2[/math]. Предположим, что [math]E^*[/math] уменьшается по модифицированному экспоненциальному закону и показатель степени при [math]\tau[/math] в общем случае неизвестен:

[math] \begin{equation} E^* = e^{-\alpha \tau^\beta}, \label{expectationTauBeta} \end{equation} [/math]

где [math]\beta[/math] — функция от [math]\sigma_v^2[/math], [math]\alpha[/math] — функция от [math]\sigma_v^2[/math] и [math]\lambda[/math].

В рамках гипотезы~(\ref{expectationTauBeta}) [math]\beta[/math] имеет определённое значение для каждого значения [math]\sigma_v^2[/math]. При [math]\sigma_v^2 = 0[/math] показатель [math]\beta = 2[/math]^[9], по мере же увеличения [math]\sigma_v^2[/math], согласно рисунку~\ref{standingWave}, величина [math]\beta[/math] должна уменьшаться.

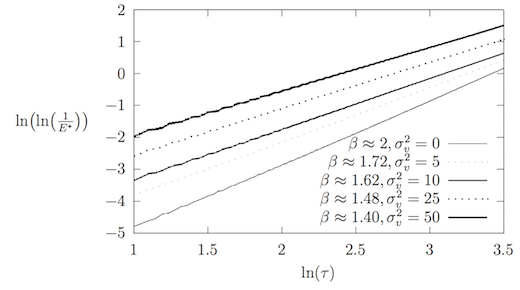
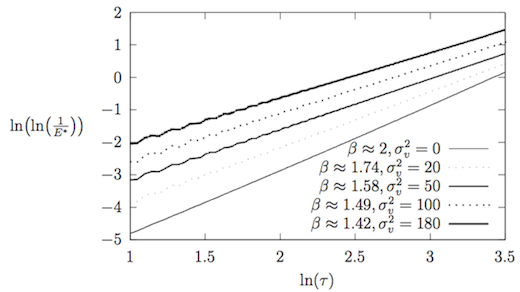
Если выражение~(\ref{expectationTauBeta}) верно, то показатель [math]\beta[/math] в зависимости от величины теплового шума можно определить, перестроив график энергии~\ref{standingWave} в логарифмических осях.

[math] \begin{equation} \begin{split} E^* & = e^{-\alpha \tau^\beta} \Rightarrow \\ \Rightarrow \ln\!\left(E^*\right) & = -\alpha \tau^\beta \Rightarrow \\ \Rightarrow \ln\!\left(-\ln\!\left(E^*\right)\right) & = \ln\!\left(\alpha \tau^\beta\right) \Rightarrow \\ \Rightarrow \ln\!\left(\ln\!\left(\frac{1}{E^*}\right)\right) & = \ln\!\left(\alpha\right) + \ln\!\left(\tau^\beta\right) \Rightarrow \\ \Rightarrow \ln\!\left(\ln\!\left(\frac{1}{E^*}\right)\right) & = \ln\!\left(\alpha\right) + \beta\ln\!\left(\tau\right). \end{split} \label{expectationTauBetaLine} \end{equation} [/math]

Обозначим [math]\ln\!\left(\tau\right)[/math] за [math]x[/math], а [math]\ln\!\left(\ln\!\left(\frac{1}{E^*}\right)\right)[/math] за [math]y[/math], тогда уравнение~(\ref{expectationTauBetaLine}) сводится к линейному. Угол наклона прямой в осях [math]\left(\ln\!\left(\tau\right); \ln\!\left(\ln\!\left(\frac{1}{E^*}\right)\right) \right)[/math], выраженный в радианах, будет численно равен [math]\beta[/math] для определённого значения дисперсии.

[math] \begin{equation} y\!\left(x\right) = \ln\!\left(\alpha\right) + \beta x \label{lineEquation} \end{equation} [/math]

Рисунок 4. Изменение механической энергии стоячей волны с течением времени в логарифмических осях

Соответствующее~(\ref{expectationTauBetaLine}) преобразование графика энергии приведено на рисунке 4. Получившиеся функции успешно аппроксимируются наклонными прямыми, что подтверждает высказанную гипотезу~(\ref{expectationTauBeta}).

Рисунок 5. Значения [math]\beta[/math] при разных значениях дисперсии, стоячая волна

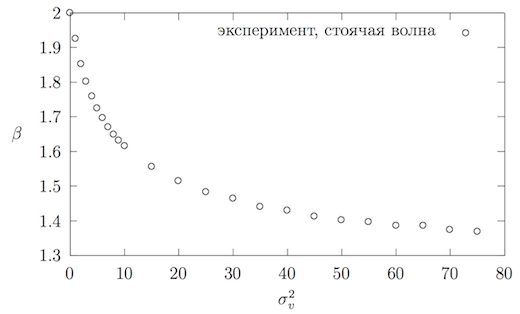
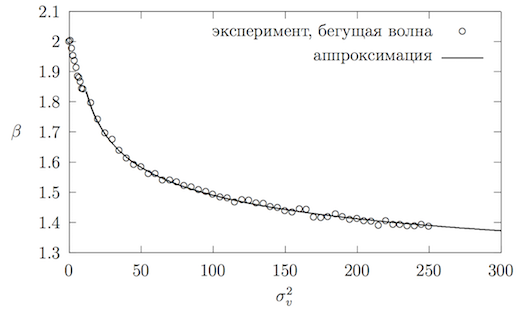
Найденные значения [math]\beta[/math] приведены на рисунке~\ref{standingWaveBeta}. Тепловая энергия в реальном материале может превосходить механическую на несколько порядков. Чтобы оценить значение [math]\beta[/math] в таком случае, построим аппроксимацию этого графика и определим предельное значение показателя при условии [math]\sigma_v^2 \rightarrow \infty[/math].

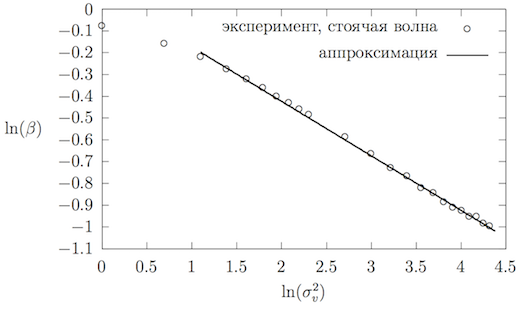
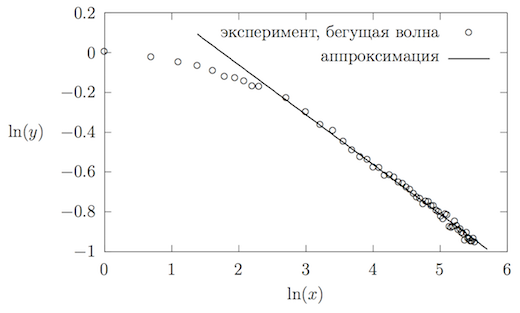
Перестроим график из осей [math]\left(\sigma_{v}^{2} ; \beta \right)[/math] в [math]\left(\ln\!\left(\sigma_{v}^{2}\right) ; \ln\!\left(\beta - 1\right) \right)[/math]. Результат приведён на рисунке~\ref{standingWaveBetaLog}. Начиная с [math]x = 1.5[/math] значения могут быть аппроксимированы прямой:

[math] \begin{equation} y\!\left(x\right) = \ln\!\left(1.08\right) - 0.25 x, \label{standingWaveApproximation} \end{equation} [/math]

где [math]x = \ln\!\left(\sigma_{v}^{2}\right)[/math], [math]y = \ln\!\left(\beta\right)[/math].

Выражая из~(\ref{standingWaveApproximation}) функцию [math]\beta[/math], получаем следующее:

[math] \begin{equation} \beta \! \left(\sigma_{v}^{2} \right) = 1 + \frac{1.08}{\sqrt[4]{\sigma_{v}^{2}}} = 1 + \frac{1.08}{\sqrt{\sigma_{v}}}, \label{standingWaveApproximation2} \end{equation} [/math]

где [math]\sigma_{v}[/math] — среднеквадратическое отклонение скоростей частиц, отнесённое к своему начальному значению (при [math]\tau~=~0[/math]).

Рисунок 6. Значения функции [math]\beta \! \left(\sigma_{v}^{2} \right)[/math] в логарифмических осях, стоячая волна

Рисунок 7. Аппроксимация графика [math]\beta[/math], стоячая волна

Рисунок 8. Аппроксимация графика [math]\beta[/math], стоячая волна

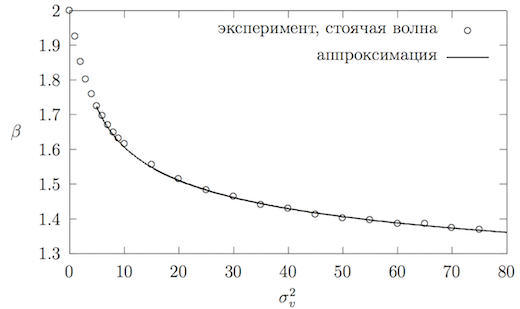
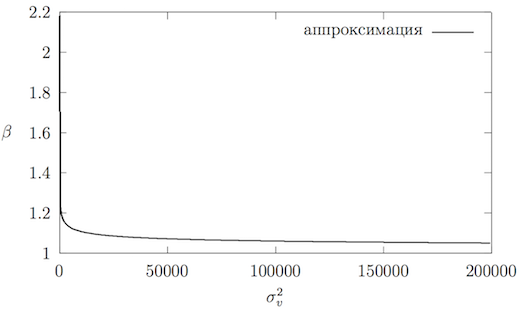
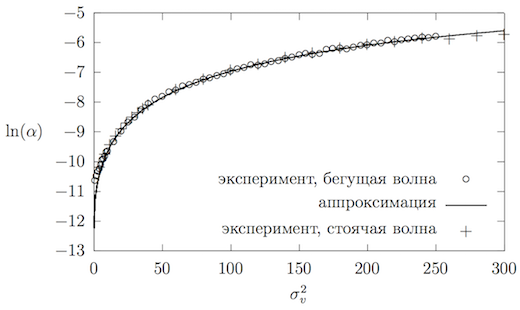
Аппроксимированный график [math]\beta[/math] от [math]\sigma_{v}^{2}[/math] приведён на рисунках 7 и 8. Найдём предельное значение [math]\beta[/math]:

[math] \begin{equation} \lim_{\sigma_{v}^{2} \to \infty} \beta \! \left(\sigma_{v}^{2} \right) = \lim_{\sigma_{v}^{2} \to \infty} 1 + \frac{1.08}{\sqrt[4]{\sigma_{v}^{2}}} = 1 + \frac{1.08}{\infty} = 1. \label{standingWaveLimit} \end{equation} [/math]

Можно считать, для больших значений [math]\sigma_{v}^{2}[/math] механическая энергия будет переходить в тепловую по закону [math]E^* = e^{-\alpha \tau}[/math]. Сходимость [math]\beta[/math] к единице также видна на рисунке~\ref{standingWaveBetaApproximation} (снизу). Уже при [math]\sigma_{v} = 12 \cdot 10^3[/math] ошибка в определении [math]\beta[/math] единицей составит менее процента.

Рисунок 9. Аппроксимация графика [math]\alpha[/math], стоячая волна

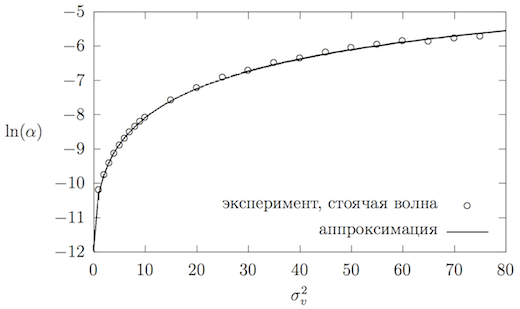
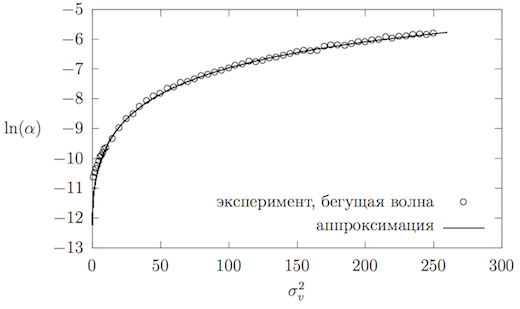
Исследуем поведение [math]\alpha[/math] в зависимости от величины теплового шума. Для этого воспользуемся уравнениями прямых, полученных аппроксимацией механической энергии [math]E^*[/math] в логарифмических осях (см. рисунок~\ref{standingWaveBetaLog}). Подставив в уравнение (\ref{lineEquation}) [math]x = 0[/math], определим значения [math]\ln\!\left(\alpha\right)[/math] как функции от [math]\sigma_{v}^{2}[/math]. Результат приведён на рисунке 9. Была получена следующая формула для аппроксимации [math]\alpha[/math]:

[math] \begin{equation} \ln\!\left(\alpha\right) = \ln\!\left(0.14\right) - \frac{50}{5 + \sqrt{\sigma_{v}^{2}}} = \ln\!\left(0.14\right) - \frac{50}{5 + \sigma_{v}}. \label{standingWaveAlpha} \end{equation} [/math]

Аналогично выражению для [math]\beta[/math], уравнение \ref{standingWaveAlpha} имеет предельное значение при [math]\sigma_{v}^{2}~\to~\infty[/math]:

[math] \begin{equation} \lim_{\sigma_{v}^{2} \to \infty} \ln\!\left(\alpha\right) = \lim_{\sigma_{v}^{2} \to \infty} \left( \ln\!\left(0.14\right) - \frac{50}{5 + \sqrt{\sigma_{v}^{2}}} \right) = \ln\!\left(0.14\right). \label{standingWaveAlphaLimit} \end{equation} [/math]

Отсюда следует, что

[math] \begin{equation} \lim_{\sigma_{v}^{2} \to \infty} \alpha = 0.14. \label{standingWaveAlphaLimit2} \end{equation} [/math]

При [math]\sigma_{v}^{2} = 12 \cdot 10^3[/math] значение [math]\alpha[/math] отличается от предельного примерно на [math]0.2\%[/math].

Дополнительное рассмотрение цепочек с кратным числом частиц привело к следующему результату: уменьшение длины кристалла в [math]2[/math] раза приводит к увеличению предельного значения [math]\alpha[/math] в [math]4[/math] раза. То есть, [math]\alpha \sim k^{2}[/math] ([math]k[/math] — волновое число, [math]k \sim \frac{1}{\lambda}[/math]). Таким образом, в реальных материалах изменение нормированной механической энергии [math]E^*[/math] может быть описано экспоненциальным законом:

[math] \begin{equation} E^*\!\left(\tau\right) = e^{-0.14 k_{*}^{2} \tau}, \label{energySolution} \end{equation} [/math]

где [math]k_{*} = \frac{k}{k_{1000}}[/math], [math]k_{1000}[/math] — значение [math]k[/math] при [math]N = 1000[/math].

Сравним полученную зависимость с решением уравнения продольных колебаний стержня с внутренним трением. В используемых обозначениях уравнение колебаний может быть записано таким образом:

[math] \begin{equation} \frac{\partial^2 u}{\partial \tau^2} = \frac{E T_{0}^{2}}{\rho a^2} \frac{\partial^2 u}{\partial x^2} + 2 \gamma \frac{\partial^3 u}{\partial \tau \partial x^2}, \label{oscillationEquation} \end{equation} [/math]

где [math]E[/math] — модуль Юнга, [math]\rho[/math] — плотность, [math]2 \gamma[/math] — безразмерный коэффициент при диссипативном члене, [math]x[/math] — безразмерная переменная расстояния.

Решение дифференциального уравнения~(\ref{oscillationEquation}) имеет вид:

[math] \begin{equation} u = \frac{A_{c}}{\omega_{c}} e^{-\gamma k_{c}^{2} \tau} \sin\!\left( \omega_{c} \tau \right) \sin\!\left( k_{c} x \right), \label{oscillationEquationSolution} \end{equation} [/math]

где [math]\omega_{c} = k_{c} \sqrt{\frac{E T_{0}^{2}}{\rho a^2} - \gamma}[/math], [math]k_{c} = \frac{a}{2} k[/math], [math]A_{c} = \frac{a}{T0} A[/math].

Данный результат был представлен в работе К. Ю. Аристовича^[10] и хорошо согласуется с формулой~(\ref{standingWaveEquation2}), переписанной в безразмерных величинах:

[math] \begin{equation} u = \frac{A_{c}}{\hat{\omega_{c}}} e^{- 0.14 k_{*}^{2} \tau} \sin\!\left( \hat{\omega_{c}} \tau \right) \sin\!\left( k_{*} x \right), \label{standingWaveEquation3} \end{equation} [/math]

где [math]\hat{\omega_{c}} = T_{0} \omega_{0}.[/math]

Сопоставим решение~(\ref{oscillationEquationSolution}) с~(\ref{standingWaveEquation3}) и определим значений [math]\gamma[/math]:

[math] \begin{equation} \gamma = 0.14 \left(\frac{k_{*}}{k_{c}} \right)^{2} = 0.14 \left( \frac{k}{k_{1000}} \frac{1}{k a} \right)^{2} = 0.14 \left(\frac{1000}{N} \frac{N}{2 \pi} \right)^{2} \approx 3550. \end{equation} [/math]

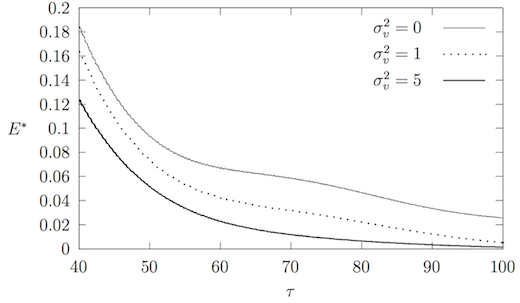
Покажем необратимость преобразования механической энергии в тепловую. Парадокс Ферми-Паста-Улама продемонстрировал явление возврата формы и механической энергии волны^[6]. Обратный переход энергии цепочки в механическую энергию был описан для одномерного нелинейного кристалла без теплового движения^[11]. Такой переход также был экспериментально получен в данной работе. Рассмотрим влияние теплового шума на этот процесс.

На рисунке 10 можно заметить дополнительный изгиб графика энергии [math]E^*\!\left(T\right)[/math] при малых значениях [math]\sigma_v^2[/math]. Так, для [math]\sigma_v^2 = 0[/math] возврат механической энергии наблюдается примерно в диапазоне от [math]\tau=60[/math] до [math]\tau=75[/math]. Для [math]\sigma_v^2 = 1[/math] этот диапазон уже: от [math]\tau=65[/math] до [math]\tau=70[/math], при этом прирост энергии значительно меньше. Для высоких значений [math]\sigma_v^2[/math] обратный переход энергии не удаётся продемонстрировать. Можно утверждать, что процесс преобразования механической энергии в тепловую в больших системах с высокими значениями отношения тепловой энергии к механической (соответствует реальным системам) является необратимым.

Рисунок 10. Изменение энергии стоячей волны

Преобразование механической энергии бегущей волны

Рассмотрим график убывания механической энергии бегущей волны с течением времени (рисунок 13). Качественно он совпадает с графиком энергии стоячей волны (рисунок 3). При отсутствии теплового шума для энергии волны также выполняется соотношение [math]E^* \sim e^{-\tau^2}[/math].

Рисунок 11. Изменение энергии бегущей волны в зависимости от [math]\tau[/math]

Чтобы найти зависимость [math]\beta\!\left(\sigma_v^2\right)[/math], аналогичным образом перестроим график энергии [math]E^{*}\!\left(\tau\right)[/math] в логарифмических осях (см. рисунок 12) и определим угол наклона [math]\beta[/math].

Рисунок 12. Изменение механической энергии стоячей волны с течением времени в логарифмических осях

Вид [math]\beta[/math] приведён на рисунке 13. Аппроксимация также была получена переводом осей [math]\left(\sigma_{v}^{2} ; \beta \right)[/math] в [math]\left(\ln\!\left(\sigma_{v}^{2}\right) ; \ln\!\left(\beta\right)\right)[/math] (см. рисунок 14).

Рисунок 13. Аппроксимация графика [math]\beta[/math], бегущая волна

Рисунок 14. Значения функции [math]\beta \! \left(\sigma_{v}^{2} \right)[/math] в логарифмических осях, бегущая волна

Для [math]\beta[/math] был получен следующий вид уравнения аппроксимации:

[math] \begin{equation} \beta \! \left(\sigma_{v}^{2} \right) = 1 + \frac{1.55}{\sqrt[4]{\sigma_{v}^{2}}} = 1 + \frac{1.55}{\sqrt{\sigma_{v}}}. \label{runningWaveApproximation} \end{equation} [/math]

При условии, что [math]\sigma_{v}^{2} \to \infty[/math], эта функция стремится к единице, аналогично аппроксимирующей функции в случае стоячей волны.

Значения [math]\alpha[/math] для различных [math]\sigma_{v}^{2}[/math] также были получены (рисунок 15). Предел аппроксимирующей функции равен соответствующему значению для аппроксимирующей функции стоячей волны. Таким образом, в реальных материалах экспоненциальная формула для механической энергии выполняется вне зависимости от типа заданной механической волны.

Рисунок 15. Значения функции [math]\alpha \! \left(\sigma_{v}^{2} \right)[/math] в логарифмических осях, бегущая волна

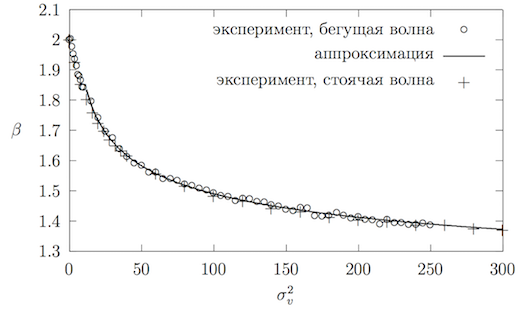
На рисунке 16 приведён график значений [math]\beta[/math] для стоячей волны, растянутый по горизонтальной оси в 4 раза. В таком масштабе экспериментальные значения [math]\beta[/math] для бегущей и стоячей волн могут быть аппроксимированы одной и той же кривой (функцией для бегущей волны). То есть, в случае бегущей волны было получено в 4 раза более медленное убывание механической энергии, чем в случае стоячей. Такая же пропорциональность наблюдается для значений [math]\alpha[/math] (см. рисунок 17).

[math] \begin{equation} \ln\!\left(\alpha\right) = \ln\!\left(0.14\right) - \frac{97.5}{9.5 + \sqrt{\sigma_{v}^{2}}} = \ln\!\left(0.14\right) - \frac{97.5}{9.5 + \sigma_{v}}. \label{runningWaveAlpha} \end{equation} [/math]

Рисунок 16. Сравнение значений [math]\beta[/math] для стоячей волны (в масштабе 4:1) и для бегущей волны

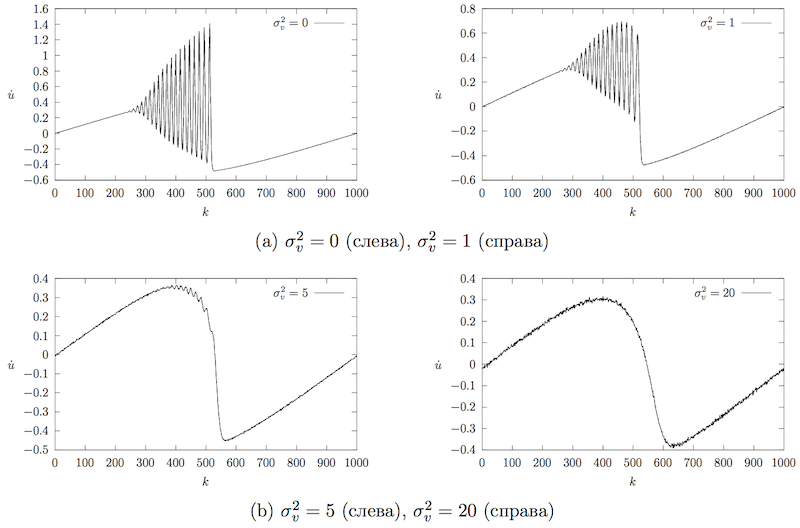
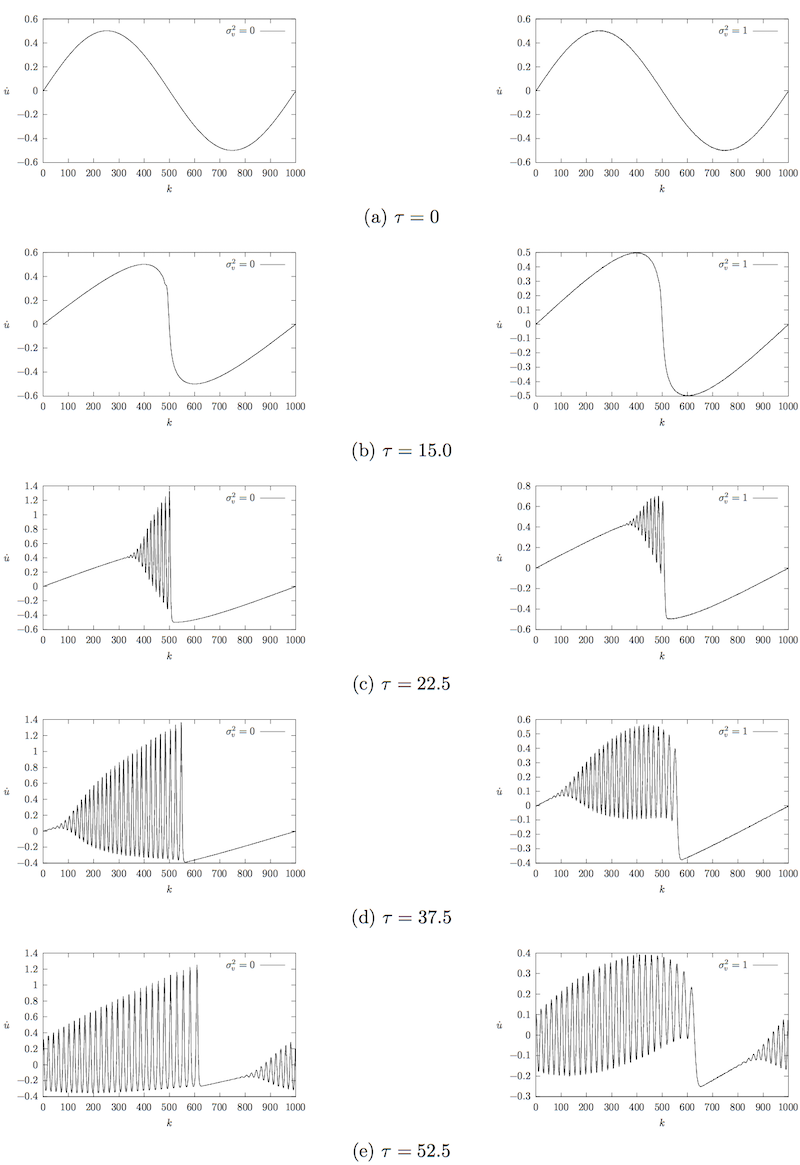
Также одним из результатов поставленных компьютерных экспериментов является обнаружение влияния теплового шума на развал скорости задаваемой механической волны. В случае нулевой дисперсии ([math]\sigma_v^2 = 0[/math]) наклон графика скорости волны возрастает вплоть до критического значения, после чего образуется дополнительный колебательный процесс (рисунок 19, слева). Свойства этого процесса были изучен^[12]. Однако увеличение [math]\sigma_v^2[/math], как было показано ранее, приводит к росту скорости убывания энергии волны и, как следствие, качественно влияет на процесс развала (рисунок 19, справа).

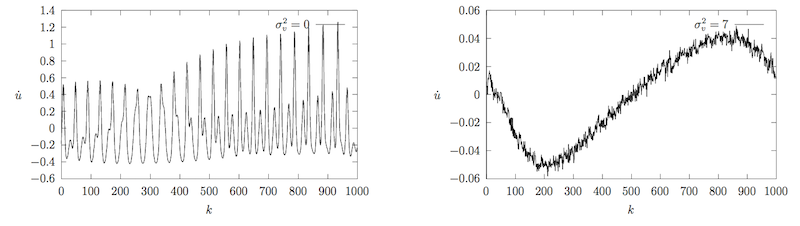
Нагляднее это влияние можно рассмотреть на рисунке 18, где приведено развитие скоростей механической волны для разных значений дисперсии по состоянию на один и тот же момент времени. При [math]\sigma_v^2 = 5[/math] побочный колебательный процесс выражен неявно, а при [math]\sigma_v^2 = 20[/math] вовсе отсутствует. Объясняется это тем, что затухание волны происходит слишком быстро, и наклон графика не достигает критического значения.

При достаточно [math]\sigma_{v}^{2}[/math] амплитуда волны продолжает падать, но форма остаётся практически неизменной. На рисунке 17 видно, что график скоростей в кристалле со значением [math]\sigma_v^2~=~7[/math] и при [math]\tau~=~115.5[/math] по форме близок к графику начального возмущения (см. рисунок 1).

Рисунок 17. Сравнение значений [math]\alpha[/math] для стоячей волны (в масштабе 4:1) и для бегущей волны

Рисунок 18. Скорость механической волны на момент [math]\tau~=~115.5[/math] для [math]\sigma_v^2~=~0[/math] (слева) и [math]\sigma_v^2~=~7[/math] (справа)

Рисунок 19. Скорость механической волны на момент [math]\tau = 27.0[/math] для разных значений [math]\sigma_v^2[/math]

Рисунок 20. Эволюция скорости механической волны для [math]\sigma_v^2~=~0[/math] (слева) и [math]\sigma_v^2~=~1[/math] (справа)

Заключение

В работе проведено исследование перехода механической энергии в тепловую в одномерном кристалле. В качестве модели кристалла рассмотрена цепочка частиц одинаковой массы. Взаимодействие между частицами нелинейное: выражения для сил содержат квадратичную зависимость от расстояния между частицами.

Начальная механическая энергия системы задана с помощью синусоидальной волны. Рассмотрены две постановки: стоячая волна и бегущая волна, распространяющаяся в одном направлении. Начальные скорости частиц определены таким образом, чтобы удовлетворить равномерному температурному профилю в начальный момент времени.

В качестве меры механической энергии системы [math]E^*[/math] взято отношение энергии волны к её начальному значению. Для проведения исследования введён безразмерный параметр [math]\sigma_v^2[/math], характеризующий величину дисперсии флуктуаций скоростей в цепочке и равный отношению тепловой энергии к механической в начале расчёта.

Заданная механическая энергия с течением времени переходит в тепловую. Продемонстрирована необратимость этого процесса, а также зависимость скорости перехода от [math]\sigma_v^2[/math]: при увеличении дисперсии механическая энергия убывает быстрее. Функция убывания описана с помощью модифицированного экспоненциального закона: [math]E^* = e^{-\alpha \tau ^{\beta}}[/math], где [math]\tau[/math] – безразмерное время процесса, [math]\beta[/math] и [math]\alpha[/math]– функции от [math]\sigma_v^2[/math].

Зависимость [math]\alpha \! \left( \sigma_v^2 \right)[/math] и [math]\beta \! \left( \sigma_v^2 \right)[/math] получены экспериментально для серии [math]\sigma_v^2[/math]. Предложены аппроксимации этих функций для стойчей и бегущей волн.

[math] \beta \! \left(\sigma_{v}^{2} \right) = 1 + \frac{1.08}{\sqrt{\sigma_{v}}}, \quad \alpha \! \left(\sigma_{v}^{2} \right) = 0.14 \exp\!\left(- \frac{50}{5 + \sigma_{v}}\right), [/math]

[math] \beta \! \left(\sigma_{v}^{2} \right) = 1 + \frac{1.55}{\sqrt{\sigma_{v}}}, \quad \alpha \! \left(\sigma_{v}^{2} \right) = 0.14 \exp\!\left(- \frac{97.5}{9.5 + \sigma_{v}}\right), [/math]

где [math]\sigma_{v}[/math] – среднеквадратическое отклонение скоростей частиц кристалла.

Показано, что энергия стоячей волны убывает в 4 раза быстрее энергии бегущей волны при одних параметрах эксперимента. Продемонстрированы предельные значения [math]\beta[/math]:

• [math]\beta = 2[/math] при [math]\sigma_v^2 = 0[/math];
• [math]\beta \rightarrow 1[/math] при [math]\sigma_v^2 \rightarrow \infty[/math].

Показано влияние скорости убывания [math]E^*[/math] на развал бегущей волны и, как следствие, образование дополнительного колебательного процесса. При больших значениях [math]\sigma_v^2[/math] волна сохраняет свою первоначальную форму, развал не происходит из-за слишком быстрого перехода механической энергии волны в тепловую.

Результаты работы были получены с использованием вычислительных ресурсов суперкомпьютерного центра Санкт-Петербургского политехнического университета Петра Великого. Каждый расчёт производился на отдельном ядре CPU с использованием технологии MPI, одновременно задействовалось [math]1000[/math] ядер. Таким образом, для получения [math]5 \cdot 10^4[/math] реализаций вычисления повторялись [math]50[/math] раз, в среднем общее время моделирования для одного значения [math]\sigma^{2}_{v}[/math] составило [math]20[/math] минут при шаге [math]\Delta t = 0.05 T_0[/math], [math]6[/math] часов при [math]\Delta t = 0.005 T_0[/math] и [math]12[/math] часов при [math]\Delta t = 0.0005 T_0[/math] ([math]T_0[/math] – заданный масштаб времени).

Автор благодарен Д. В. Цветкову за полезные обсуждения.

Список литературы

1. ↑ Yenny et al. Hernandez. High-yield production of graphene by liquid-phase exfoliation of graphite. Nature Nanotechnology, 3:563–568, 2008.
2. ↑ Xiaolin et al. Li. Highly conducting graphene sheets and langmuir-blodgett films. Nature Nanotechnology, 3:538–542, 2008.
3. ↑ L. Shi et al. Evaluating broader impacts of nanoscale thermal transport research. Nanoscale and Microscale Thermophysical Engineering, 19:127–165, 2015.
4. ↑ Kostya S Novoselov, Andre K Geim, Sergei V Morozov, D Jiang, Y Zhang, Sergey V Dubonos, Irina V Grigorieva, and Alexandr A Firsov. Electric field effect in atomically thin carbon films. Science, 306(5696):666–669, 2004.
5. ↑ Z. Xu, G. Tai, Y. Zhou, F. Gao, and K. H. Wong. Self-charged graphene battery harvests electricity from thermal energy of the environment. ArXiv e-prints, 2012.
6. ↑ ^{6,0 6,1 6,2} Enrico Fermi, J. Pasta, and S. Ulam. Studies of nonlinear problems. Los Alamos Report LA-1940, 978, 1965.
7. ↑ A. M. Krivtsov. Energy distribution in one-dimensional crystal. Dokl. Phys. 60 (9), page 407, 2015.
8. ↑ A. M. Krivtsov. On unsteady heat conduction in a harmonic crystal. ArXiv e-prints, September 2015.
9. ↑ ^{9,0 9,1} D. V. Tsvetkov and A. M. Krivtsov. Energy distribution in one-dimensional crystal. Book of papers 24th International Congress of Theoretical and Applied Mechanics, pages 2450–2451, 2016.
10. ↑ К. Ю. Аристович. Зависимость макроскопических параметров колебаний кристаллического стержня от микроструктуры. Труды XXI международной конференции «Математическое моделирование в механике сплошных сред. Методы граничных и конечных элементов», 2:23–35, 2006.
11. ↑ Д. В. Цветков. Распределение тепла в одномерном кристалле. Диссертация магистра, pages 19–23, 2015.
12. ↑ С. Д. Александров. Исследование свойств солитона в нелинейном одномерном кристалле. Выпускная квалификационная работа, pages 13–18, 2016.