Динамическая потеря устойчивости стержня при сжатии (простейшая модель) — различия между версиями
| Строка 38: | Строка 38: | ||
<center> | <center> | ||
| − | {{#widget:Iframe|url=https://ailurus.ru/stands/buckling/?iframe|width=680|height= | + | {{#widget:Iframe|url=https://ailurus.ru/stands/buckling/?iframe|width=680|height=550|border=0}} |
</center> | </center> | ||
==Результаты== | ==Результаты== | ||
| − | + | Здесь приведены конечные результаты, при заданных начальных параметрах. | |
| + | |||
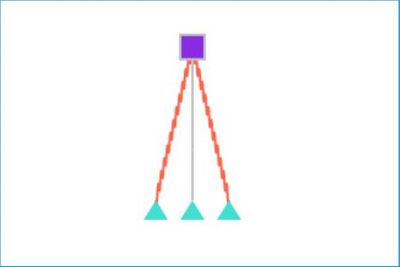
| + | На Рисунке 2 предоставлено конечное положение грузика, при заданном времени. | ||
| + | |||
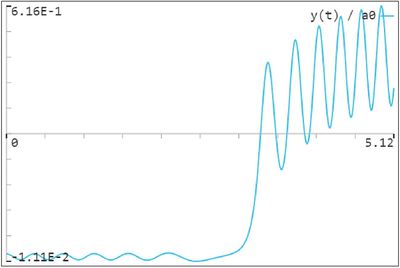
| + | На Графике 1 мы наблюдаем, что на некотором расстоянии между стенками (через | ||
| + | некоторое время после начала движения стен) равновесие становится неустойчивым. | ||
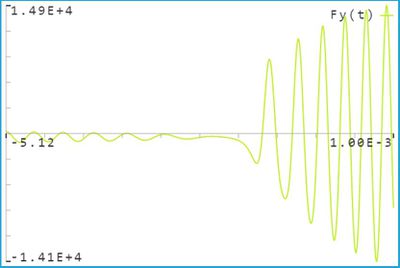
| + | На Графике 2 мы видим проекцию результируещей силы во времени на ось <math>{Y}</math> | ||
| − | |||
| − | |||
| − | |||
| + | [[Файл:KonPolGr.JPG|thumb|Рисунок 2|центр|400px]] | ||
| + | [[Файл:Y(t).JPG|thumb|График 1. '''<math>{\pmb Y}(t)</math>''' |слева|400px]] | ||
| + | [[Файл:Fy(t).JPG|thumb|График 2. '''<math>{\pmb F_{y}}(t)</math>''' |справа|400px]] | ||
| + | С помощью графика <math>{\pmb Y}(t)</math> можно наблюдать переход колебаний с одного устойчивого положения на другое | ||
Версия 23:37, 11 января 2017
Курсовые работы 2016-2017 учебного года > Динамическая потеря устойчивости стержня при сжатии (простейшая модель)Курсовой проект по Механике дискретных сред
Исполнитель: Филимонов Александр
Группа: 09 (43604/1)
Семестр: осень 2016
Формулировка задачи
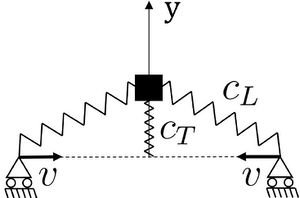
1) Смоделировать стержень как показано на Рисунке 1.
2) Построить график , где - проекция результирующей на ось , - время.
3) Построить график , где - координата "грузика", - время.
3) Иметь возможность менять исходные параметры.
Общие сведения
Для моделирования рассмотрим простую одномерную модель, которая отражает основные физические характеристики стержня подвергающегося сжатию с постоянной скоростью. Стержень моделируется с помощью грузика, двух пружин и двух опор("стен"). Грузик связан с двумя стенками линейными пружинами с жесткостью . Поперечная жесткость стержня моделируется пружиной с жесткостью . "Стены" движутся навстречу друг другу с постоянной скоростью .
Программа
В данной программе в начальный момент времени задаются:
Жесткости пружин = и = .
Начальное отклонение грузика от положения равновесия().
Масса грузика ()
Результаты
Здесь приведены конечные результаты, при заданных начальных параметрах.
На Рисунке 2 предоставлено конечное положение грузика, при заданном времени.
На Графике 1 мы наблюдаем, что на некотором расстоянии между стенками (через некоторое время после начала движения стен) равновесие становится неустойчивым.
На Графике 2 мы видим проекцию результируещей силы во времени на ось
С помощью графика можно наблюдать переход колебаний с одного устойчивого положения на другое
Ссылки
- Vitaly A. Kuzkin Structural model for the dynamic buckling of a column under constant rate compression