Динамическая потеря устойчивости стержня при сжатии (простейшая модель) — различия между версиями

Материал из Department of Theoretical and Applied Mechanics
Перейти к: навигация, поиск
(→‎Формулировка задачи)
Строка 26: Строка 26:
 
линейными пружинами с жесткостью <math>{\pmb с_{L}}</math>. Поперечная жесткость стержня моделируется пружиной с  
 
линейными пружинами с жесткостью <math>{\pmb с_{L}}</math>. Поперечная жесткость стержня моделируется пружиной с  
 
жесткостью <math>{\pmb с_{T}}</math>. "Стены" движутся навстречу друг другу с постоянной скоростью <math>{\pmb v}</math>.
 
жесткостью <math>{\pmb с_{T}}</math>. "Стены" движутся навстречу друг другу с постоянной скоростью <math>{\pmb v}</math>.
 +
 +
 +
==Программа==
 +
В данной программе в начальный момент времени задаются:
 +
 +
жесткости пружин <math>{\pmb k_{1}}</math> = <math>{\pmb с_{L}}</math> и <math>{\pmb k_{2}}</math> = <math>{\pmb с_{T}}</math>.
 +
 +
ные скорости(начальная энергия,они достаточно велики, чтобы можно было пренебречь потенциальной энергией взаимодействия. Можно менять количество молекул углекислого газа и сбрасывать таймер расчета средних значений. Так же выводятся:кинетическая энергия системы в данный момент времени, средняя кинетическая энергия системы в данный момент времени, средние энергии, приходящиеся на атом углерода, первый и второй атом кислорода в молекуле.
 +
*Красные шары - атомы углерода
 +
*Синие шары - атомы кислорода
 +
 +
<center>
 +
{{#widget:Iframe|url=https://ailurus.ru/stands/buckling/?iframe|width=638|height=535|border=0}}
 +
 +
<big>[//ailurus.ru/stands/buckling/ Страница полного решения]</big>
 +
</center>

Версия 21:36, 11 января 2017

Курсовые работы 2016-2017 учебного года > Динамическая потеря устойчивости стержня при сжатии (простейшая модель)

Курсовой проект по Механике дискретных сред

Исполнитель: Филимонов Александр

Группа: 09 (43604/1)

Семестр: осень 2016


Формулировка задачи

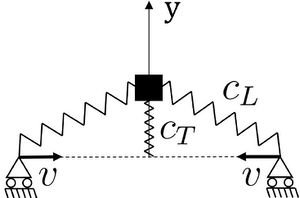
Рис.1 Структурная модель для динамического прогиба стержня при постоянной скорости сжатия.

1) Смоделировать стержень как показано на Рисунке 1.

2) Построить график [math]{\pmb F_{y}}(t)[/math], где [math]{\pmb F_{y}}[/math] - проекция результирующей на ось [math]{Y}[/math], [math]{t}[/math] - время.

3) Построить график [math]{\pmb Y}(t)[/math], где [math]{Y}[/math] - координата "грузика", [math]{t}[/math] - время.

3) Иметь возможность менять исходные параметры.

Общие сведения

Для моделирования рассмотрим простую структурную модель, которая отражает основные физические характеристики стержня подвергающегося сжатию с постоянной скоростью. Стержень моделируется с помощью частиц (грузик) связан с двумя стенками линейными пружинами с жесткостью [math]{\pmb с_{L}}[/math]. Поперечная жесткость стержня моделируется пружиной с жесткостью [math]{\pmb с_{T}}[/math]. "Стены" движутся навстречу друг другу с постоянной скоростью [math]{\pmb v}[/math].


Программа

В данной программе в начальный момент времени задаются:

жесткости пружин [math]{\pmb k_{1}}[/math] = [math]{\pmb с_{L}}[/math] и [math]{\pmb k_{2}}[/math] = [math]{\pmb с_{T}}[/math].

ные скорости(начальная энергия,они достаточно велики, чтобы можно было пренебречь потенциальной энергией взаимодействия. Можно менять количество молекул углекислого газа и сбрасывать таймер расчета средних значений. Так же выводятся:кинетическая энергия системы в данный момент времени, средняя кинетическая энергия системы в данный момент времени, средние энергии, приходящиеся на атом углерода, первый и второй атом кислорода в молекуле.

  • Красные шары - атомы углерода
  • Синие шары - атомы кислорода

Страница полного решения

Источник — «http://tm.spbstu.ru/?title=Динамическая_потеря_устойчивости_стержня_при_сжатии_(простейшая_модель)&oldid=45790»