Обратный каскад энергии(двумерная турбулентность) — различия между версиями
(→top) |
(→top) |
||
| Строка 8: | Строка 8: | ||
где m, r - масса и радиус вектор i-ой частицы, <math>{{}^p}{\pmb F_{ij}}, {{}^d}{\pmb F_{ij}}</math> - отталкивающая потенциальная и диссипативная силы соответственно. | где m, r - масса и радиус вектор i-ой частицы, <math>{{}^p}{\pmb F_{ij}}, {{}^d}{\pmb F_{ij}}</math> - отталкивающая потенциальная и диссипативная силы соответственно. | ||
| − | <big><math>\ | + | Выражения для потенциальной и диссипативной сил: |
| + | |||
| + | <big><math> | ||
| + | {{}^p}{\pmb F_{ij}} = | ||
| + | \begin{cases} | ||
| + | \frac{6D}{a^{2}}{\left(\frac{a_{c} - \pmb r_{ij}}{a_{c} - a}\right)}^{2}{\left(\frac{a}{\pmb r_{ij}}\right)}^{10}, & \text{если} \; \pmb r_{ij} \leqslant a_{c}; \\ | ||
| + | 0, & \text{если} \; \pmb r_{ij} > a_{c}. | ||
| + | \end{cases} | ||
| + | </math></big> | ||
| + | |||
| + | <big><math> | ||
| + | {{}^d}{\pmb F_{ij}} = | ||
| + | \begin{cases} | ||
| + | \beta {\left(\frac{a_{c} - \pmb r_{ij}}{a_{c} - a}\right)}^{2} \left( \pmb v_{j} - \pmb v_{i}\right)\cdot \pmb e_{ij} \pmb e_{ij} , & \text{если} \; \pmb r_{ij} \leqslant a_{c}; \\ | ||
| + | 0, & \text{если} \; \pmb r_{ij} > a_{c}. | ||
| + | \end{cases} | ||
| + | </math></big> | ||
==Программа== | ==Программа== | ||
==Анализ== | ==Анализ== | ||
==Ссылки== | ==Ссылки== | ||
Версия 23:21, 15 декабря 2016
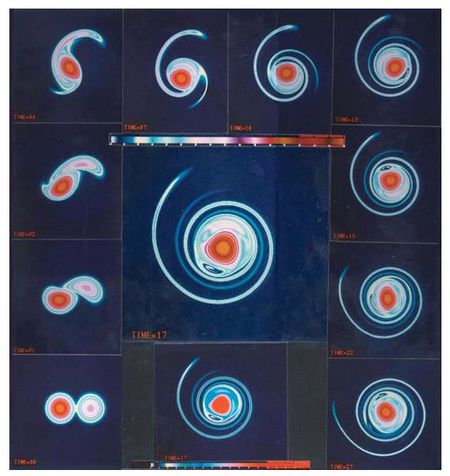
Переход энергии с микро на макро уровень (и обратно) - одно из фундаментальных физических явлений. В данной работе,на примере двумерных турбулентных вихрей, рассматривается случай перехода с мелкомасштабного механического движения на крупномасштабное. В литературе это явление обычно упоминается как “обратный каскад” энергии. Построенная модель позволяет исследовать переход энергии с микро на макро уровень и корреляции скоростей в дискретной среде.
Модель представлена набором взаимодействующих частиц с случайными начальными скоростями. Частицы взаимодействуют за счет отталкивающих потенциальных и диссипативных сил. Динамика взаимодействия описана набором уравнений движения Ньютона:
где m, r - масса и радиус вектор i-ой частицы, - отталкивающая потенциальная и диссипативная силы соответственно.
Выражения для потенциальной и диссипативной сил: