Колебания материальной точки в поле силы тяжести — различия между версиями
Материал из Department of Theoretical and Applied Mechanics
(бла) |
|||
| Строка 12: | Строка 12: | ||
\right. | \right. | ||
</math> | </math> | ||
| + | |||
| + | ==Реализация== | ||
| + | {{#widget:Iframe |url=http://tm.spbstu.ru/htmlets/Lobas/yiis.html |width=1200 |height=1650 |border=0 }} | ||
| + | |||
| + | |||
| + | ==Ссылки== | ||
| + | *Разработчик : [[Лобас Анна]] | ||
| + | * [[Виртуальная лаборатория]] | ||
| + | *[https://bitbucket.org/Sasha_Kozulski/project-4-th-semester Посмотреть код] | ||
Версия 11:56, 25 октября 2016
Виртуальная лаборатория > Колебания материальной точки в поле силы тяжестиКраткое описание системы
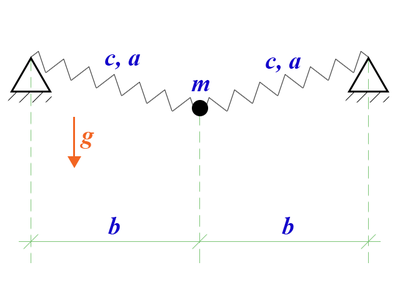
Рассмотрим механическую систему с двумя степенями свободы: материальная точка массы связана пружинами с двумя опорами, вся система находится в поле силы тяжести. Расстояние между опорами , длина пружин в недеформированном состоянии , жесткость пружин .
Уравнения движения системы будут выглядеть так:
Реализация
Ссылки
- Разработчик : Лобас Анна
- Виртуальная лаборатория
- Посмотреть код