Колебания материальной точки в поле силы тяжести — различия между версиями
Материал из Department of Theoretical and Applied Mechanics
| Строка 7: | Строка 7: | ||
\left\{ | \left\{ | ||
\begin{array}{ll} | \begin{array}{ll} | ||
| − | m \ddot{x} = \frac {c(a+x)} | + | m \ddot{x} = -\frac {c(a+x)}{y}(a-\sqrt{y^{2}+(a+x)^{2}})-\frac {c(a-x)}{\sqrt{y^{2}+(a+x)^{2}}}(a-\sqrt{y^{2}+(a-x)^{2}})\\ |
\displaystyle m \ddot{y} = -\frac {cy}{\sqrt{y^{2}+(a+x)^{2}}}(a-\sqrt{y^{2}+(a+x)^{2}})-\frac {cy}{\sqrt{y^{2}+(a+x)^{2}}}(a-\sqrt{y^{2}+(a-x)^{2}})+mg\\ | \displaystyle m \ddot{y} = -\frac {cy}{\sqrt{y^{2}+(a+x)^{2}}}(a-\sqrt{y^{2}+(a+x)^{2}})-\frac {cy}{\sqrt{y^{2}+(a+x)^{2}}}(a-\sqrt{y^{2}+(a-x)^{2}})+mg\\ | ||
\end{array} | \end{array} | ||
\right. | \right. | ||
</math> | </math> | ||
Версия 21:55, 6 октября 2016
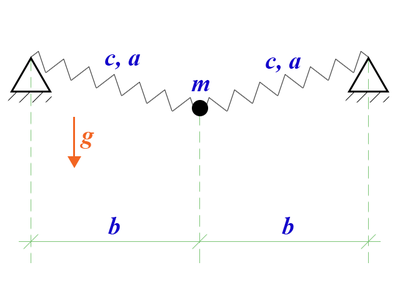
Виртуальная лаборатория > Колебания материальной точки в поле силы тяжестиКраткое описание системы
Рассмотрим механическую систему с двумя степенями свободы: материальная точка массы связана пружинами с двумя опорами, вся система находится в поле силы тяжести. Расстояние между опорами , длина пружин в недеформированном состоянии , жесткость пружин .
Уравнения движения системы будут выглядеть так: