Моделирование движения системы двойной звезды — различия между версиями
Anpolol (обсуждение | вклад) (→Аннотация работа) |
Anpolol (обсуждение | вклад) (→Постановка задачи) |
||
| Строка 12: | Строка 12: | ||
==Постановка задачи== | ==Постановка задачи== | ||
| − | + | *Изучить взаимодействие звёзд в системе двойной звезды. | |
| − | + | *Написать программу на C++ моделирующую движение звёзд в системе методом численного интегрирования Верле. | |
==Общие сведения== | ==Общие сведения== | ||
Версия 18:02, 17 июня 2016
Курсовая работа по информатике
Исполнитель:Андреева Полина
Группа:13604/1
Семестр: весна 2016
Содержание
Аннотация к работе
Данная работа посвящена моделированию траектории движения звёзд в системе двойной звезды методом численного интегрирования Верле. Также была добавлена планета в систему и смоделирована её траектория без влияния её присутствия на траекторию звёзд.
Постановка задачи
- Изучить взаимодействие звёзд в системе двойной звезды.
- Написать программу на C++ моделирующую движение звёзд в системе методом численного интегрирования Верле.
Общие сведения
Кратная звездная система - это система из двух или более звезд, находящихся в постоянной взаимной гравитационной зависимости. Одиночная звезда — вещь труднопознаваемая. Изучая двойные системы, астрономы получают возможность определять важнейшие характеристики объекта: его массу, радиус, температуру, светимость и т.п. Программа сохраняет координаты движения звезд в файл. При написании программы я использовала метод численного интегрирования Верле для нахождения следующей координаты траектории, зная текущее и предыдущее значение:
x(t+Δt)=2x(t)-x(t-Δt)+ax(t)Δt^2 y(t+Δt)=2y(t)-y(t-Δt)+ay(t)Δt^2
Ускорение считается из формулы второго закона Ньютона, а сила из закона гравитации:
F(t)=G*m1*m2/r^2; a(t)=F(t)/m;
графики строила в программе gnuplot.
Выводы
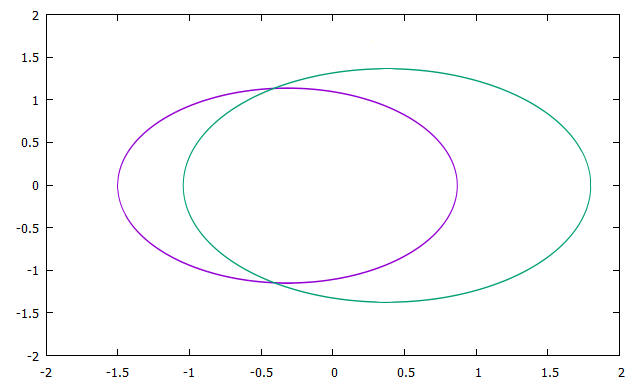
Программа моделирует движение системы двойной звезды, ниже представлены графики траекторий:
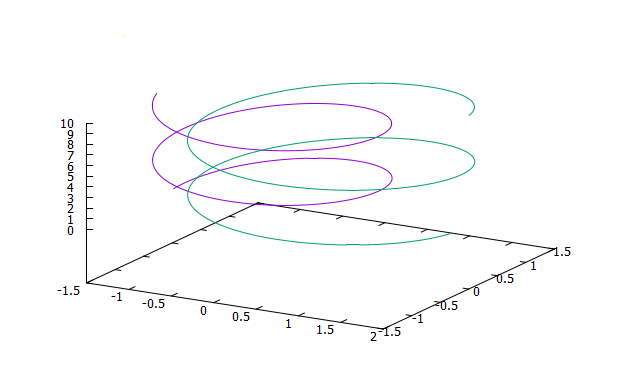
трехмерное движение:
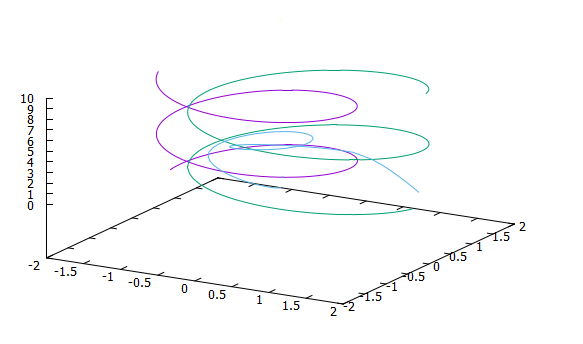
Также добавлена планета(фиолетовая и зеленая линия-звезды, голубая-планета.):
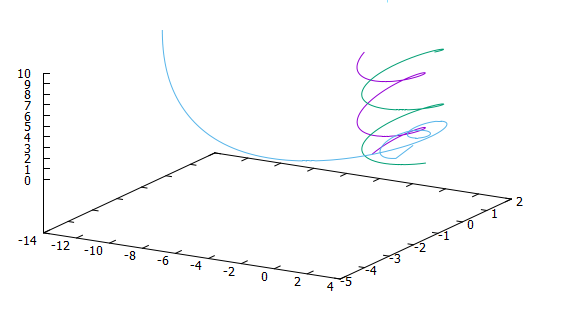
И рассмотрен вариант когда планета имеет большую скорость и улетает из системы двойной звезды:
Список литературы
1.Мороз В.И., Кононович Э.В., общий курс астрономии: Учебное пособие/под ред. В.В.Иванова. Изд. 2-е, испр.
2.http://www.astronet.ru/db/msg/1188258
3.http://www.allkosmos.ru/dvojnye-i-kratnye-zvezdy/
4.http://spacegid.com/dvoynyie-zvezdyi.html
Курсовая
скачать работу