Моделирование броуновского движения — различия между версиями
Loban9614 (обсуждение | вклад) (→Список литературы) |
Loban9614 (обсуждение | вклад) (→Ссылки) |
||
| Строка 59: | Строка 59: | ||
==Ссылки== | ==Ссылки== | ||
| − | [[:File:Kursovaya rabota Lobanov Ilya.rar|Cкачать программу и | + | [[:File:Kursovaya rabota Lobanov Ilya.rar|Cкачать программу и отчёт]] |
Версия 16:47, 17 июня 2016
Курсовой проект по информатике
Исполнитель: Лобанов Илья
Группа: 13604/1
Семестр: весна 2016
Содержание
Аннотация к проекту
Данная курсовая работа посвящена изучению движения броуновской частицы под воздействием атомов или молекул, из которых состоит газ, непрерывно толкающих данную частицу со всех сторон.
Постановка задачи
- Написать программу, моделирующую движение броуновской частицы в газе.
- Рассмотреть влияние летающих молекул на движение броуновской частицы.
Основные определения и понятия
Броуновское движение происходит из-за того, что все жидкости и газы состоят из атомов или молекул — мельчайших частиц, которые находятся в постоянном хаотическом тепловом движении, и потому непрерывно толкают броуновскую частицу с разных сторон. Было установлено, что крупные частицы с размерами более 5 мкм в броуновском движении практически не участвуют (они неподвижны или седиментируют), более мелкие частицы (менее 3 мкм) двигаются поступательно по весьма сложным траекториям или вращаются. Когда в среду погружено крупное тело, то толчки, происходящие в огромном количестве, усредняются и формируют постоянное давление. Если крупное тело окружено средой со всех сторон, то давление практически уравновешивается, остаётся только подъёмная сила Архимеда — такое тело плавно всплывает или тонет. Если же тело мелкое, как броуновская частица, то становятся заметны флуктуации давления, которые создают заметную случайно изменяющуюся силу, приводящую к колебаниям частицы. Броуновские частицы обычно не тонут и не всплывают, а находятся в среде во взвешенном состоянии.
Результаты работы программы
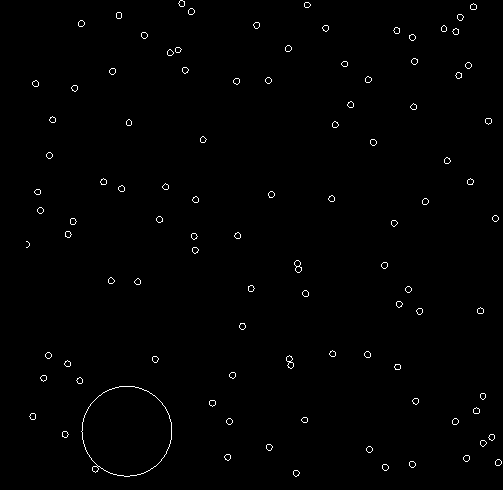
1) Положение броуновской частицы в момент времени t=0
2) Положение броуновской частицы в произвольный момент времени
Список литературы
Роберт Лафоре Объектно-ориентированное программирование в C++, 4-е издание (2004)
Непрерывное равномерное распределение
http://av-physics.narod.ru/molecule/molecular-movement.htm