Силовой резонанс для осциллятора с диссипацией — различия между версиями
(Новая страница: ««Силовой резонанс для осциллятора с диссипацией» "Курсовой проект по информатике" ""Вып…») |
|||
| Строка 1: | Строка 1: | ||
| − | + | '''Силовой резонанс для осциллятора с диссипацией''' | |
| − | + | Курсовой проект по информатике | |
| − | + | Исполнитель: [[Васильева Анастасия]] | |
| − | + | Группа 13604/1 | |
| + | Кафедра Теоретической механики | ||
| + | |||
| + | Семестр: весна 2016 | ||
| − | |||
==Аннотация проекта== | ==Аннотация проекта== | ||
| + | |||
Явление резонанса играет очень большую роль в динамике, его исследованию посвящено большое число работ. Здесь мы ограничимся разбором наиболее простой ситуации резонанса для одномерного гармонического осциллятора. | Явление резонанса играет очень большую роль в динамике, его исследованию посвящено большое число работ. Здесь мы ограничимся разбором наиболее простой ситуации резонанса для одномерного гармонического осциллятора. | ||
| + | |||
| + | |||
| + | ==Мотивировки и постановка задачи== | ||
| + | |||
| + | Одномерный гармонический осциллятор является модельной системой, на которой можно наблюдать основные явления, связанные с колебаниями. При этом, вообще говоря, колебательные явления могут иметь весьма различную природу: колебания параметров орбит планет, звуковые явления, осцилляции токов в электрических цепях, колебания численности популяций животных и т. д. Кроме того, известно, что во многих реальных ситуациях существенное влияние на динамику оказывает диссипация – утечка энергии из колебательного движения в другие ее формы. Поэтому целесообразно рассмотреть в качестве модельной системы осциллятор с диссипацией (сохраняя, разумеется, возможность задать ее малой или даже нулевой). | ||
| + | |||
| + | ==Исследование задачи с помощью программы== | ||
| + | Приступим к обсуждению характера динамики, возникающей в нашей системе в различных ситуациях. | ||
| + | Сначала рассмотрим случай отсутствия трения: 𝛾=0. При этом возьмем собственную частоту осциллятора 𝜔0=1, а частоту внешней силы 𝜔=5, то есть зададим их далекими друг от друга. | ||
| + | [[File:y=0,w0=1,w=5.png]] | ||
| + | Видим, что динамика представляет собой суперпозицию двух колебаний: резкие зигзаги соответствуют колебанию с высокой частотой, а воображаемая более плавная кривая, на которую они "нанизаны" – колебанию с меньшей частотой. | ||
| + | Зададим теперь значения частот, более близкие друг к другу: ω0=1,ω=1.2. | ||
| + | [[File:y=0,w0=1,w=1,2.png]] | ||
| + | Динамика приобретает характер колебания с медленно меняющейся амплитудой (также совершающей колебания). Такой процесс называют биениями. | ||
| + | Рассмотрим теперь случай полного (точного) резонанса: ω0=ω=1. | ||
| + | [[File:y=0,w0=w=1.png]] | ||
| + | Происходит колебание с линейно растущей амплитудой. | ||
| + | Обратимся теперь к случаю ненулевого трения: 𝛾≠0. Сначала рассмотрим случай, когда ε>γ, например, ω0=1,ω=1.2,γ=0.03. | ||
| + | [[File:y=0,03,w0=1,w=1,2.png]] | ||
| + | Видно, что происходят колебания, амплитуда которых, в свою очередь, осциллирует, и ее осцилляции постепенно затухают. Процесс приближается к режиму обычных гармонических колебаний, которые в этом случае называются установившимися колебаниями. Изображенную динамику называют переходным процессом, или процессом установления колебаний. | ||
| + | Теперь рассмотрим случай, когда трение "превалирует" над удалением от резонанса: ε « γ, например, ω0 =1,ω = 1.0001,γ=0.05. [[File:y=0,05,w0=1,w=1,0001.png]] | ||
| + | Здесь мы имеем переходный процесс с плавно возрастающей амплитудой, которая стремится к некоторой константе – амплитуде установившихся колебаний. | ||
| + | Таким образом, при наличии трения динамика содержит переходный процесс, на протяжении которого затухают вызванные внешней силой свободные колебания (на собственной частоте осциллятора), а также последующие установившиеся вынужденные колебания. | ||
| + | |||
| + | |||
| + | ==Заключение== | ||
| + | |||
| + | Явление силового резонанса является важнейшим проявлением действия внешних сил на колебательные системы. Через него устанавливается соотношение между частотой воздействующей на осциллятор силы и собственной частотой осциллятора: как мы видели, резонанс, то есть существенное возрастание амплитуды колебаний, происходит, когда эти частоты близки друг к другу. Иначе говоря, система сильно поглощает энергию тех воздействий, которые происходят на близких к ее собственным | ||
| + | частотах, и пропускает другие воздействия. Это свойство имеет широчайшие проявления в природе и применения в технике. | ||
| + | Так, оно лежит в основе радиотехники, акустических приборов и музыкальных инструментов, лазерной техники. Более экзотические примеры включают орбитальный резонанс, из-за которого, например, периоды орбит трех из четырех галилеевских спутников Юпитера – Ганимеда, Европы и Ио – относятся как 4:2:1 (так называемый резонанс Лапласа), а также приливный | ||
| + | резонанс, приводящий к резкому усилению приливов в бухтах, где их период совпадает со временем прохождения бухты длинной волной. Кроме того, резонансные явления, хотя и несколько своеобразной, квантовой природы, лежат в основе многих методов изучения вещества. В этом случае внешние воздействия резонируют с параметрами систем атомного масштаба. Например, так устроены оптическая и инфракрасная спектроскопии газов, эффект Мёссбауэра, магнитный резонанс. Следует также отметить, что во многих ситуациях резонансы могут иметь нежелательные для человека последствия: разрушение мостов, башен, механических устройств. Все это делает изучение резонансных явлений одной из центральных областей внимания исследователей. | ||
==Список литературы== | ==Список литературы== | ||
| Строка 20: | Строка 54: | ||
5. «Объектно-ориентированное программирование в С++» Р. Лафоре | 5. «Объектно-ориентированное программирование в С++» Р. Лафоре | ||
| − | + | Общие сведения, а также саму программу можно скачать по ссылке: | |
[[:File:Проект1.zip]] | [[:File:Проект1.zip]] | ||
Версия 12:45, 17 июня 2016
Силовой резонанс для осциллятора с диссипацией
Курсовой проект по информатике
Исполнитель: Васильева Анастасия
Группа 13604/1 Кафедра Теоретической механики
Семестр: весна 2016
Содержание
Аннотация проекта
Явление резонанса играет очень большую роль в динамике, его исследованию посвящено большое число работ. Здесь мы ограничимся разбором наиболее простой ситуации резонанса для одномерного гармонического осциллятора.
Мотивировки и постановка задачи
Одномерный гармонический осциллятор является модельной системой, на которой можно наблюдать основные явления, связанные с колебаниями. При этом, вообще говоря, колебательные явления могут иметь весьма различную природу: колебания параметров орбит планет, звуковые явления, осцилляции токов в электрических цепях, колебания численности популяций животных и т. д. Кроме того, известно, что во многих реальных ситуациях существенное влияние на динамику оказывает диссипация – утечка энергии из колебательного движения в другие ее формы. Поэтому целесообразно рассмотреть в качестве модельной системы осциллятор с диссипацией (сохраняя, разумеется, возможность задать ее малой или даже нулевой).
Исследование задачи с помощью программы
Приступим к обсуждению характера динамики, возникающей в нашей системе в различных ситуациях.
Сначала рассмотрим случай отсутствия трения: 𝛾=0. При этом возьмем собственную частоту осциллятора 𝜔0=1, а частоту внешней силы 𝜔=5, то есть зададим их далекими друг от друга.
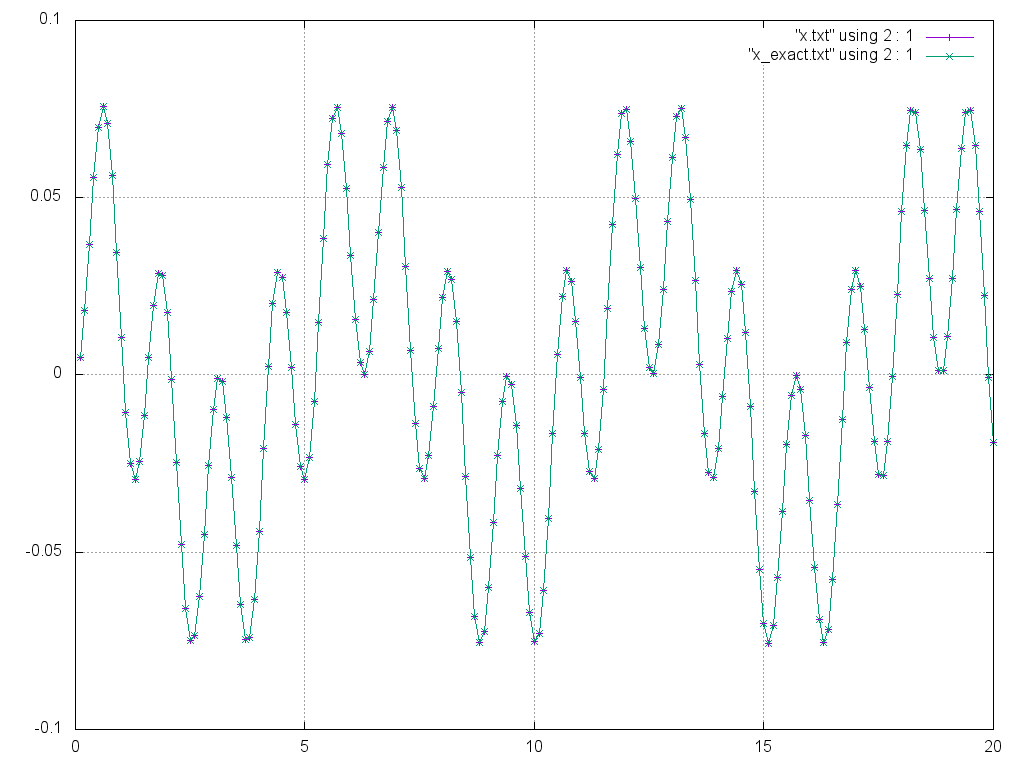 Видим, что динамика представляет собой суперпозицию двух колебаний: резкие зигзаги соответствуют колебанию с высокой частотой, а воображаемая более плавная кривая, на которую они "нанизаны" – колебанию с меньшей частотой.
Зададим теперь значения частот, более близкие друг к другу: ω0=1,ω=1.2.
Видим, что динамика представляет собой суперпозицию двух колебаний: резкие зигзаги соответствуют колебанию с высокой частотой, а воображаемая более плавная кривая, на которую они "нанизаны" – колебанию с меньшей частотой.
Зададим теперь значения частот, более близкие друг к другу: ω0=1,ω=1.2.
 Динамика приобретает характер колебания с медленно меняющейся амплитудой (также совершающей колебания). Такой процесс называют биениями.
Рассмотрим теперь случай полного (точного) резонанса: ω0=ω=1.
Динамика приобретает характер колебания с медленно меняющейся амплитудой (также совершающей колебания). Такой процесс называют биениями.
Рассмотрим теперь случай полного (точного) резонанса: ω0=ω=1.
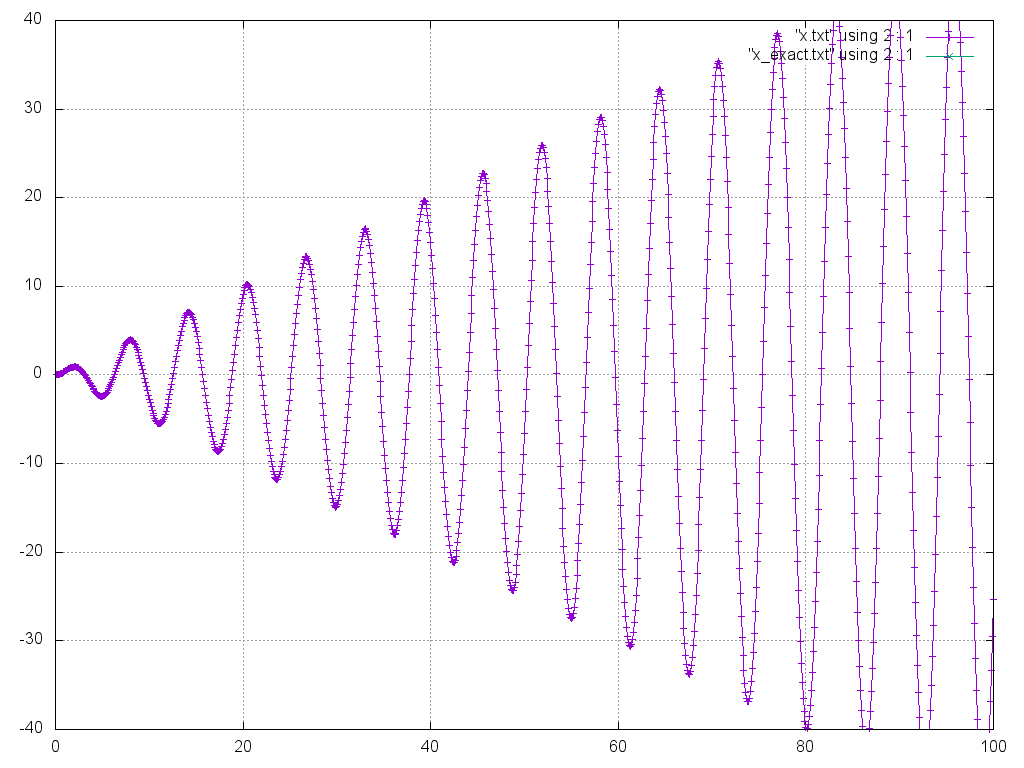 Происходит колебание с линейно растущей амплитудой.
Обратимся теперь к случаю ненулевого трения: 𝛾≠0. Сначала рассмотрим случай, когда ε>γ, например, ω0=1,ω=1.2,γ=0.03.
Происходит колебание с линейно растущей амплитудой.
Обратимся теперь к случаю ненулевого трения: 𝛾≠0. Сначала рассмотрим случай, когда ε>γ, например, ω0=1,ω=1.2,γ=0.03.
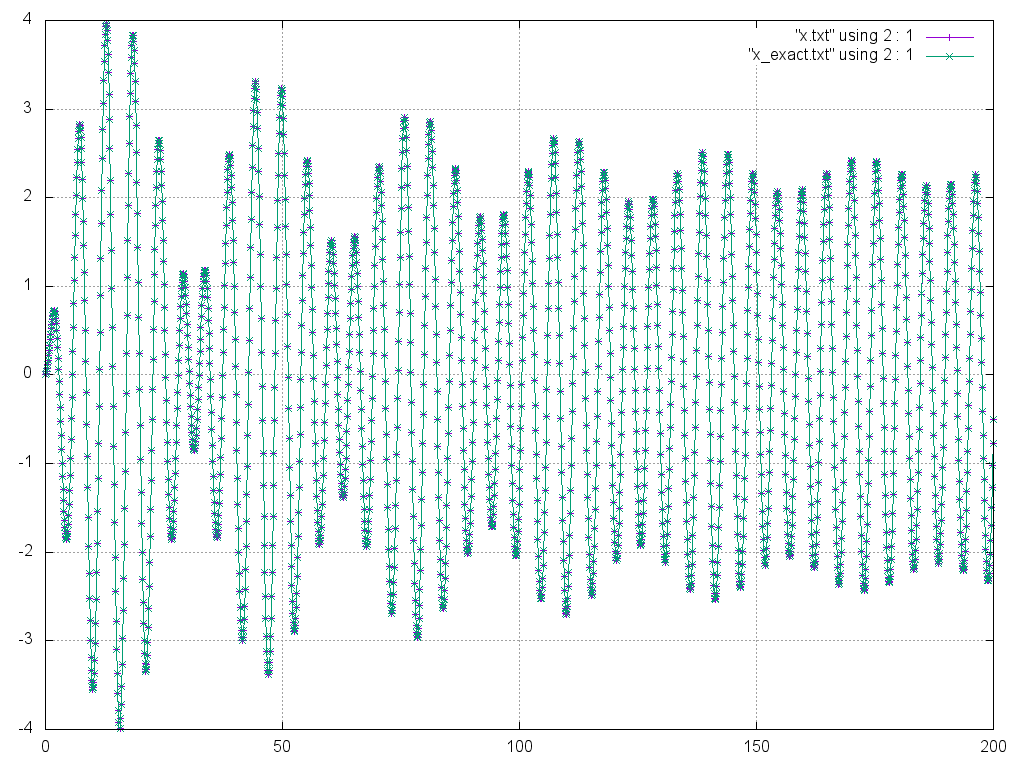 Видно, что происходят колебания, амплитуда которых, в свою очередь, осциллирует, и ее осцилляции постепенно затухают. Процесс приближается к режиму обычных гармонических колебаний, которые в этом случае называются установившимися колебаниями. Изображенную динамику называют переходным процессом, или процессом установления колебаний.
Теперь рассмотрим случай, когда трение "превалирует" над удалением от резонанса: ε « γ, например, ω0 =1,ω = 1.0001,γ=0.05.
Видно, что происходят колебания, амплитуда которых, в свою очередь, осциллирует, и ее осцилляции постепенно затухают. Процесс приближается к режиму обычных гармонических колебаний, которые в этом случае называются установившимися колебаниями. Изображенную динамику называют переходным процессом, или процессом установления колебаний.
Теперь рассмотрим случай, когда трение "превалирует" над удалением от резонанса: ε « γ, например, ω0 =1,ω = 1.0001,γ=0.05. 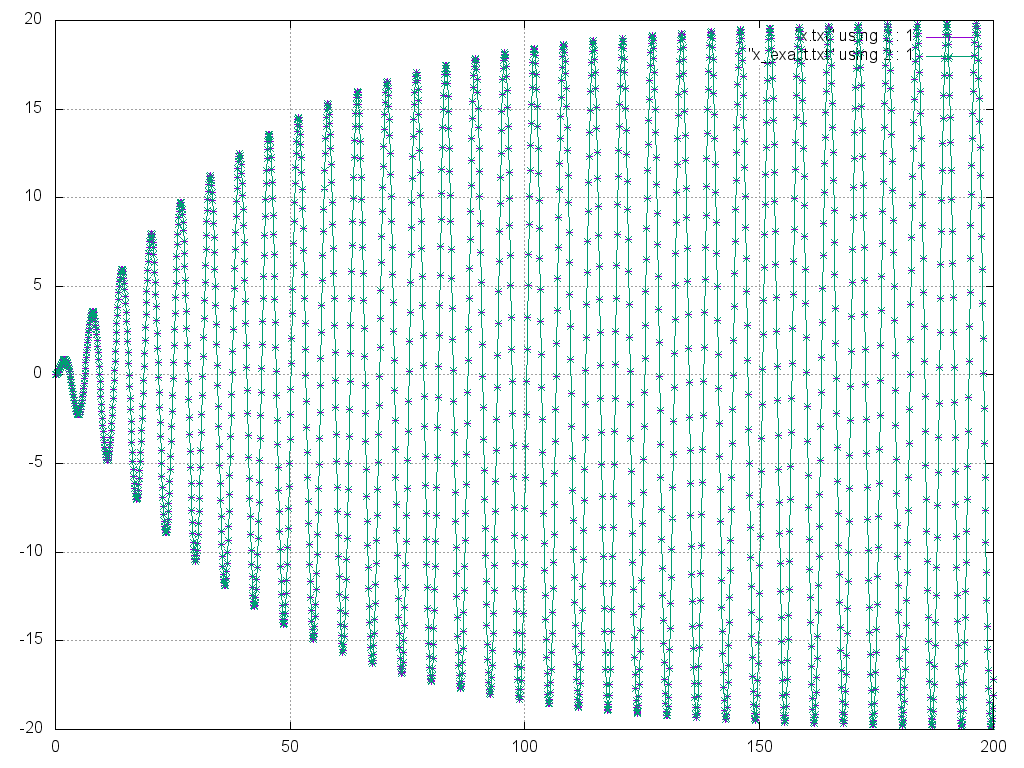 Здесь мы имеем переходный процесс с плавно возрастающей амплитудой, которая стремится к некоторой константе – амплитуде установившихся колебаний.
Таким образом, при наличии трения динамика содержит переходный процесс, на протяжении которого затухают вызванные внешней силой свободные колебания (на собственной частоте осциллятора), а также последующие установившиеся вынужденные колебания.
Здесь мы имеем переходный процесс с плавно возрастающей амплитудой, которая стремится к некоторой константе – амплитуде установившихся колебаний.
Таким образом, при наличии трения динамика содержит переходный процесс, на протяжении которого затухают вызванные внешней силой свободные колебания (на собственной частоте осциллятора), а также последующие установившиеся вынужденные колебания.
Заключение
Явление силового резонанса является важнейшим проявлением действия внешних сил на колебательные системы. Через него устанавливается соотношение между частотой воздействующей на осциллятор силы и собственной частотой осциллятора: как мы видели, резонанс, то есть существенное возрастание амплитуды колебаний, происходит, когда эти частоты близки друг к другу. Иначе говоря, система сильно поглощает энергию тех воздействий, которые происходят на близких к ее собственным частотах, и пропускает другие воздействия. Это свойство имеет широчайшие проявления в природе и применения в технике. Так, оно лежит в основе радиотехники, акустических приборов и музыкальных инструментов, лазерной техники. Более экзотические примеры включают орбитальный резонанс, из-за которого, например, периоды орбит трех из четырех галилеевских спутников Юпитера – Ганимеда, Европы и Ио – относятся как 4:2:1 (так называемый резонанс Лапласа), а также приливный резонанс, приводящий к резкому усилению приливов в бухтах, где их период совпадает со временем прохождения бухты длинной волной. Кроме того, резонансные явления, хотя и несколько своеобразной, квантовой природы, лежат в основе многих методов изучения вещества. В этом случае внешние воздействия резонируют с параметрами систем атомного масштаба. Например, так устроены оптическая и инфракрасная спектроскопии газов, эффект Мёссбауэра, магнитный резонанс. Следует также отметить, что во многих ситуациях резонансы могут иметь нежелательные для человека последствия: разрушение мостов, башен, механических устройств. Все это делает изучение резонансных явлений одной из центральных областей внимания исследователей.
Список литературы
1. http://www.cyberforum.ru/ 2. О. М. Огородникова Вычислительные методы в компьютерном инжиниринге 3. Т.И. ЧЕРНЫШОВА, В.А. ТЁТУШКИН МОДЕЛИРОВАНИЕ В РАДИОЭЛЕКТРОННЫХ СРЕДСТВАХ 4. ХУТОРОВА О.Г. СТЕНИН Ю.М. ФАХРТДИНОВ Р.Х. МОРОЗОВА Л.В. ЖУРАВЛЕВ А.А. ТЕПЛОВ В.Ю. ЗЫКОВ Е.Ю. КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ ФИЗИЧЕСКИХ ПРОЦЕССОВ 5. «Объектно-ориентированное программирование в С++» Р. Лафоре
Общие сведения, а также саму программу можно скачать по ссылке: File:Проект1.zip