Моделирование колебаний резонаторов на основе углеродных вискеров — различия между версиями
Валентина (обсуждение | вклад) (→Введение) |
|||
| Строка 7: | Строка 7: | ||
Целью данной работы является исследование динамики нановискеров с целью их оптимального применения в наноэлектромеханических системах, путем нахождения деформаций и напряжений различных наноструктур, для улучшение качеств дальнейших экспериментов, а так же подбор идеальных параметров конструкций и материалов.Это поможет значительно сократить количество неудачных экспериментов, а так же выявить новые свойства наноструктур, которые не были выявлены в ходе эксперимента. Так же с помощью данных моделирований становится более понятна природа и виды колебаний и деформаций, вызванных ими. | Целью данной работы является исследование динамики нановискеров с целью их оптимального применения в наноэлектромеханических системах, путем нахождения деформаций и напряжений различных наноструктур, для улучшение качеств дальнейших экспериментов, а так же подбор идеальных параметров конструкций и материалов.Это поможет значительно сократить количество неудачных экспериментов, а так же выявить новые свойства наноструктур, которые не были выявлены в ходе эксперимента. Так же с помощью данных моделирований становится более понятна природа и виды колебаний и деформаций, вызванных ими. | ||
Во всех последующих расчетах в качестве параметров материала вискеров взяты параметры аморфного углерода:<math> E=2\cdot 10^{10} </math>Па - модуль Юнга, <math> \rho=2200 </math> кг/м<math>^3 </math> - плотность. При этом известно, что аморфный углерод - изотропный материал, а это значит, что его физические и механические свойства не зависят от направления. | Во всех последующих расчетах в качестве параметров материала вискеров взяты параметры аморфного углерода:<math> E=2\cdot 10^{10} </math>Па - модуль Юнга, <math> \rho=2200 </math> кг/м<math>^3 </math> - плотность. При этом известно, что аморфный углерод - изотропный материал, а это значит, что его физические и механические свойства не зависят от направления. | ||
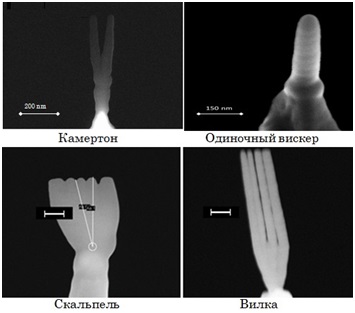
| + | [[File:Whisker.jpg|framed|left|Некоторые виды вискеров]] | ||
==Простейшие колебательные системы== | ==Простейшие колебательные системы== | ||
Версия 14:34, 17 ноября 2015
БАКАЛАВРСКАЯ РАБОТА
Автор работы: Ванюшкина Валентина
Научный руководитель: И.Е. Беринский
Введение
Нановискеры - структуры, полученные из аморфного углерода, длина которых не превышает сотни микрометров. Могут быть разных форм и размеров и применятся как наноинструменты. Целью данной работы является исследование динамики нановискеров с целью их оптимального применения в наноэлектромеханических системах, путем нахождения деформаций и напряжений различных наноструктур, для улучшение качеств дальнейших экспериментов, а так же подбор идеальных параметров конструкций и материалов.Это поможет значительно сократить количество неудачных экспериментов, а так же выявить новые свойства наноструктур, которые не были выявлены в ходе эксперимента. Так же с помощью данных моделирований становится более понятна природа и виды колебаний и деформаций, вызванных ими. Во всех последующих расчетах в качестве параметров материала вискеров взяты параметры аморфного углерода:Па - модуль Юнга, кг/м - плотность. При этом известно, что аморфный углерод - изотропный материал, а это значит, что его физические и механические свойства не зависят от направления.
Простейшие колебательные системы
Для представления колебаний одиночного вискера, наращенного на игле, было использовано моделирование механических систем с двумя степенями свободы. Это позволяет приближенно оценить колебания данной наносистемы и найти ее первые две собственные частоты. Задача о представлении вискера, прикрепленного к игле, была разделена на две подзадачи: о продольных колебаниях и поперечных колебаниях системы. Поскольку исследуемый объект состоит из двух тел, то логично представить его в виде системы с двумя степенями свободы. Очевидно, что в реальности степеней свободы будет бесконечное множество, но для нахождения первых двух собственных частот, достаточно рассмотреть упрощенную модель. Решения, полученные для данной задачи представленны в виде интерактивных моделей: Простейшая колебательная система с двумя степенями свободы и Колебания двойного маятника