Квазиодномерный кристалл — различия между версиями
Kuzkin (обсуждение | вклад) (Новая страница: «Кафедра ТМ > Научный справочник > Механика > МДС > О…») |
Kuzkin (обсуждение | вклад) (→Нелинейное, немонотонное тепловое расширение) |
||
| Строка 28: | Строка 28: | ||
* Растянутая цепочка | * Растянутая цепочка | ||
<math> | <math> | ||
| − | + | p_T \sim E_T,\qquad A > a,~~A\neq A_{*} | |
</math> | </math> | ||
| Строка 41: | Строка 41: | ||
</math> | </math> | ||
| − | Здесь | + | Здесь <math>A_{*}</math> - среднее расстояние между частицами, при котором коэффициент Грюнайзена обращается в ноль. |
== Теплопроводность == | == Теплопроводность == | ||
Текущая версия на 19:20, 18 июля 2015
Кафедра ТМ > Научный справочник > Механика > МДС > Одномерный кристалл > Квазиодномерный кристалл
Содержание
Определение[править]
В настоящей статье квазиодномерным называется кристалл, в котором частицы упорядочены в одномерную цепочку, однако движение частиц осуществляется как в продольном, так и в поперечном направлении. Взаимодействия между частицами описываются парным потенциалом .
Линейное тепловое расширение[править]
При малых тепловых энергиях зависимость давления (средней продольной силы) от тепловой энергии обычно описывается уравнением состояния Ми-Грюнайзена:
Параметр , называемый коэффициентом Грюнайзена, для квазиодномерной цепочки является суммой двух слагаемых, соответствующих продольным и поперечным колебаниям цепочки:
Для большинства потенциалов , поэтому продольные колебания вносят положительный вклад в давление, т.е. приводят к положительному тепловому расширению. Поперечные колебания, наоборот, приводят к отрицательному тепловому расширению. Данный эффект реализуется, например, в графене.
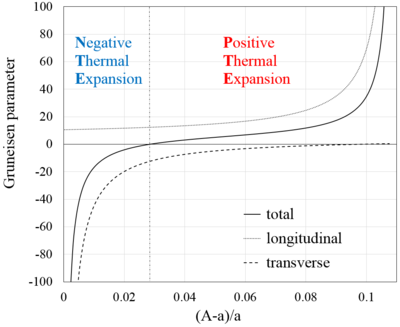
Зависимость коэффициента Грюнайзена от деформации кристалла приведена на рисунке справа. Видно, что при изменении деформации коэффициент Грюнайзена меняется в пределах от до .
Нелинейное, немонотонное тепловое расширение[править]
При некоторых деформациях цепочки уравнение состояния Ми-Грюнайзена теряет смысл. При этом необходимо пользоваться нелинейными по тепловой энергии уравнениями состояниями. Для квазиодномерного кристалла такое уравнение состояния было получено в статье В.А. Кузькина и А.М. Кривцова. Уравнение имеет достаточно сложный вид, однако из него следует, что при малых тепловых энергиях зависимость давления от тепловой энергий имеет одну из следующих асимптотик:
- Растянутая цепочка
- Нерастянутая цепочки
- Растяжение, соответствующее нулевому коэффициенту Грюнайзена
Здесь - среднее расстояние между частицами, при котором коэффициент Грюнайзена обращается в ноль.
Теплопроводность[править]
В работе [Physical Review E, 82 (1), 2010] показано, что подобно другим одномерным системам квазиодномерный кристалл не описывается законом Фурье. Коэффициент теплопроводности зависит от числа частиц .
Публикации по теме[править]
- Kuzkin V.A., Krivtsov A.M. Nonlinear positive/negative thermal expansion and equations of state of a chain with longitudinal and transverse vibrations. Physica Status Solidi b, 252, No. 7, pp. 1664–1670, 2015, DOI: 10.1002/pssb.201451618 (download author's copy)
- Santhosh G., Deepak Kumar Anomalous transport and phonon renormalization in a chain with transverse and longitudinal vibrations. Physical Review E, 82 (1), 2010.