КП: Эффект Магнуса — различия между версиями

Версия 11:49, 3 июня 2015

Курсовой проект по Теоретической механике

Исполнитель: Шварёв Николай

Группа: 09 (23604)

Семестр: весна 2015

Сила Магнуса^[1]

Аннотация проекта

Данный проект посвящен изучению эффекта Магнуса, возникающего в различных видах спорта, а также использующегося в баллистике, летательных аппаратах и кораблях.В ходе работы над проектом были рассмотрены траектории полета мяча и цилиндра в зависимости от различных начальных параметров (радиуса, динамической вязкости среды, плотности воздуха, линейной и угловой скорости). Программа написана на языке JavaScript с использование библиотеки Three.js.

Формулировка задачи

Построение и исследование математической модели движения объекта (в нашем случае - футбольного мяча и цилиндра), получение уравнения его движения и построение траектории в трехмерном пространстве с учётом различных внешних факторов, влияющих на движение, таких как сила сопротивления воздуха и эффект Магнуса.

Общие сведения по теме

Пример влияния силы Магнуса на траекторию движения мяча[1]

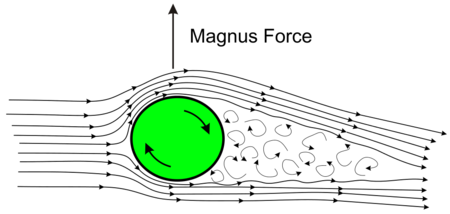
Эффект Магнуса - образование подъемной силы, действующей на вращающееся тело при обтекании его потоком жидкости или газа, широко использующейся в спорте, баллистике, летательных аппаратах и кораблях. ^[2]

Данный эффект возникает в результате разности давлений (в соответствии с законом Бернулли^[3]) на стенках объекта из-за разных скоростей движения воздуха. Возникающий дисбаланс заставляет объект отклоняться.

Решение

Силу сопротивления воздуха для мяча будем считать с помощью закона Стокса^[4]:

[math]\vec{F} = -6πrη\vec{v} [/math] , где

[math]\vec{F}[/math] - сила Стокса,

[math]r[/math] - радиус мяча,

[math]η[/math] - динамическая вязкость среды,

[math]\vec{v}[/math] - скорость мяча.

Силу Магнуса примем вида^[5]:

[math]\vec{F} = 2Sρr\vec{u}\times\vec{ω} [/math] , где

[math]\vec{F}[/math] - сила Магнуса,

[math]S[/math] - площадь действия силы,

[math]ρ[/math] - плотность воздуха,

[math]r[/math] - радиус,

[math]\vec{u}[/math] - относительная скорость,

[math]\vec{ω}[/math] - угловая скорость.

Применив метод Эйлера, получим формулы для нахождения скорости и координаты мяча:

[math] \begin{cases} v_x^{i+1} = v_x^i + (-6πrηv_x^i/m + 2Sρr(u_y^iω_z - u_z^iω_y)/m)\Delta t \\ v_y^{i+1} = v_y^i + (-6πrηv_y^i/m + 2Sρr(u_z^iω_w - u_x^iω_z)/m)\Delta t \\ v_z^{i+1} = v_z^i + (-6πrηv_z^i/m - g + 2Sρr(u_x^iω_y - u_y^iω_x)/m)\Delta t \\ \end{cases} [/math]

[math] \begin{cases} x^{i+1} = x^i + v_x^i\Delta t \\ y^{i+1} = y^i + v_y^i\Delta t \\ z^{i+1} = z^i + v_z^i\Delta t \\ \end{cases} [/math]

Реализация алгоритма.

Возможности программы:

• поочередный запуск мяча и цилиндра,
• изменение параметров как в начале, так и во время полета,
• просмотр картинки в трехмерном изображении с помощью мыши
• сброс всех данных до начальных при нажатии кнопки "Reload"

Обсуждение результатов и выводы

Пример траектории мяча

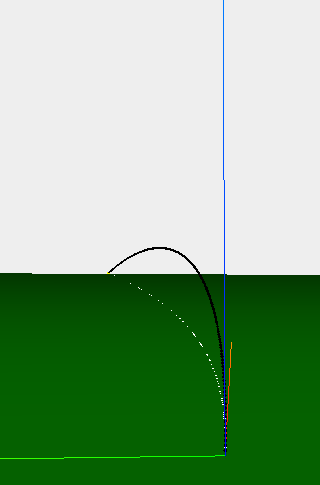
Разработанный алгоритм был реализован в среде программирования Javascript с использование библиотеки Three.js. Была построена траектория движения и произведены эксперименты, результаты которых находятся в таблице ниже:

Шар:

Цилиндр:

где [math]V_x[/math], [math]V_y[/math], [math]V_z[/math] - начальные линейные скорости, [math]ω_x[/math], [math]ω_y[/math], [math]ω_z[/math] - начальные угловые скорости, [math]m[/math] - масса объекта, [math]r[/math] - радиус объекта, [math]h[/math] - высота цилиндра, а [math]Δ_y[/math] - полученное смещение по оси [math]y[/math].

Исходя из числовых данных, полученных после проведения экспериментов, можно сделать вывод, что при большей массе скорость меньше. Это объясняется тем, что на объект большей массы действует большая сила тяжести, препятствующая движению объекта. Также видим, что при уменьшении радиуса смещение уменьшается. Это объясняется тем, что на объект с меньшим радиусом действует меньшая разность давлений при вращении, и, следственно, меньшая сила Магнуса.

Скачать отчет: doc.
Скачать презентацию: pptx.

Ссылки по теме

См. также

• Справочная информация
• Курсовые проекты ТМ