Колебания груза на пружине — различия между версиями

Материал из Department of Theoretical and Applied Mechanics
Перейти к: навигация, поиск
Строка 309: Строка 309:
 
<math>\frac{d}{dt}\left(\frac{\partial T}{\partial\dot q_i}\right) - \frac{\partial T}{\partial q_i} = \frac{\partial \Pi}{\partial y}</math>;
 
<math>\frac{d}{dt}\left(\frac{\partial T}{\partial\dot q_i}\right) - \frac{\partial T}{\partial q_i} = \frac{\partial \Pi}{\partial y}</math>;
  
−
<math>m\dot\dot y + \frac{ca^2y}{l^2} - mg = 0</math>;
+
<math>m\dot v + \frac{ca^2y}{l^2} - mg = 0</math>;
  
 
== См. также ==
 
== См. также ==

Версия 12:49, 26 мая 2015

Задача: С помощью языка программирования JavaScript смоделировать колебания груза на пружине.

Система блоков с грузом (A — грузик, a - расстояние до пружины, l - расстояние до грузика, c - жесткость пружины.)

Решение

Программа: скачать

Текст программы на языке JavaScript:

Файл "5.js" 

  1 function main()
  2 {
  3 	var step = 0;
  4 	var rr = new THREE.WebGLRenderer();
  5     rr.setSize(window.innerWidth, window.innerHeight);
  6 	rr.setClearColor(0xFFFFFFF,1);
  7     document.body.appendChild(rr.domElement);
  8     camera = new THREE.PerspectiveCamera(45, window.innerWidth / window.innerHeight, 1, 500);
  9     camera.position.set(0, 0, 100);
 10     camera.lookAt(new THREE.Vector3(0, 0, 0));
 11     var scene = new THREE.Scene();
 12 	
 13 	var material = new THREE.LineBasicMaterial({color: 0x000000});
 14 	var material1 = new THREE.LineBasicMaterial({color: 0xbbbbbb});
 15 	
 16 	var radius = 5;
 17 	var segments = 32;
 18 
 19 	var circleGeometry = new THREE.CircleGeometry(radius, segments);				
 20 	var circle = new THREE.Mesh(circleGeometry, material1);
 21 	
 22 	var radius1 = 0.5;
 23 	var segments1 = 32;
 24 
 25 	var circleGeometry = new THREE.CircleGeometry(radius1, segments1);				
 26 	var circle1 = new THREE.Mesh(circleGeometry, material);
 27 	
 28 	var geometry = new THREE.Geometry();
 29     geometry.vertices.push(new THREE.Vector3(-40, 20, 0));
 30     geometry.vertices.push(new THREE.Vector3(0, 20, 0));
 31 	
 32 	var line = new THREE.Line(geometry, material);
 33 	line.geometry.verticesNeedUpdate = true;
 34 	geometry.dynamic = true;
 35 	
 36  	var geometry1 = new THREE.Geometry();
 37     geometry1.vertices.push(new THREE.Vector3(-28, 28, 0));
 38     geometry1.vertices.push(new THREE.Vector3(-28, 27, 0));
 39 	
 40 	var line1 = new THREE.Line(geometry1, material);
 41 	line1.geometry.verticesNeedUpdate = true;
 42 	geometry1.dynamic = true; 
 43 	
 44 	var geometry2 = new THREE.Geometry();
 45     geometry2.vertices.push(new THREE.Vector3(-30, 22, 0));
 46     geometry2.vertices.push(new THREE.Vector3(-26, 21, 0));
 47 	
 48 	var line2 = new THREE.Line(geometry2, material);
 49 	line2.geometry.verticesNeedUpdate = true;
 50 	geometry2.dynamic = true;
 51 	
 52 	var geometry3 = new THREE.Geometry();
 53     geometry3.vertices.push(new THREE.Vector3(-26, 23, 0));
 54     geometry3.vertices.push(new THREE.Vector3(-30, 22, 0));
 55 	
 56 	var line3 = new THREE.Line(geometry3, material);
 57 	line3.geometry.verticesNeedUpdate = true;
 58 	geometry3.dynamic = true;
 59 	
 60 	var geometry4 = new THREE.Geometry();
 61     geometry4.vertices.push(new THREE.Vector3(-30, 24, 0));
 62     geometry4.vertices.push(new THREE.Vector3(-26, 23, 0));
 63 	
 64 	var line4 = new THREE.Line(geometry4, material);
 65 	line4.geometry.verticesNeedUpdate = true;
 66 	geometry4.dynamic = true;
 67 	
 68 	var geometry5 = new THREE.Geometry();
 69     geometry5.vertices.push(new THREE.Vector3(-26, 25, 0));
 70     geometry5.vertices.push(new THREE.Vector3(-30, 24, 0));
 71 	
 72 	var line5 = new THREE.Line(geometry5, material);
 73 	line5.geometry.verticesNeedUpdate = true;
 74 	geometry5.dynamic = true;
 75 	
 76 	var geometry6 = new THREE.Geometry();
 77     geometry6.vertices.push(new THREE.Vector3(-30, 26, 0));
 78     geometry6.vertices.push(new THREE.Vector3(-26, 25, 0));
 79 	
 80 	var line6 = new THREE.Line(geometry6, material);
 81 	line6.geometry.verticesNeedUpdate = true;
 82 	geometry6.dynamic = true;
 83 	
 84 	var geometry7 = new THREE.Geometry();
 85     geometry7.vertices.push(new THREE.Vector3(-26, 27, 0));
 86     geometry7.vertices.push(new THREE.Vector3(-30, 26, 0));
 87 	
 88 	var line7 = new THREE.Line(geometry7, material);
 89 	line7.geometry.verticesNeedUpdate = true;
 90 	geometry7.dynamic = true;
 91 	
 92 	var geometry8 = new THREE.Geometry();
 93     geometry8.vertices.push(new THREE.Vector3(-28, 28, 0));
 94     geometry8.vertices.push(new THREE.Vector3(-26, 27, 0));
 95 	
 96 	var line8 = new THREE.Line(geometry8, material);
 97 	line8.geometry.verticesNeedUpdate = true;
 98 	geometry8.dynamic = true;
 99 	
100 	var geometry9 = new THREE.Geometry();
101     geometry9.vertices.push(new THREE.Vector3(-30, 28, 0));
102     geometry9.vertices.push(new THREE.Vector3(-26, 28, 0));
103 	
104 	var line9 = new THREE.Line(geometry9, material);
105 	
106 	var geometry10 = new THREE.Geometry();
107     geometry10.vertices.push(new THREE.Vector3(-30, 28, 0));
108     geometry10.vertices.push(new THREE.Vector3(-29, 30, 0));
109 	
110 	var line10 = new THREE.Line(geometry10, material);
111 
112 	var geometry11 = new THREE.Geometry();
113     geometry11.vertices.push(new THREE.Vector3(-29, 28, 0));
114     geometry11.vertices.push(new THREE.Vector3(-28, 30, 0));
115 	
116 	var line11 = new THREE.Line(geometry11, material);
117 	
118 	var geometry12 = new THREE.Geometry();
119     geometry12.vertices.push(new THREE.Vector3(-28, 28, 0));
120     geometry12.vertices.push(new THREE.Vector3(-27, 30, 0));
121 	
122 	var line12 = new THREE.Line(geometry12, material);
123 	
124 	var geometry13 = new THREE.Geometry();
125     geometry13.vertices.push(new THREE.Vector3(-27, 28, 0));
126     geometry13.vertices.push(new THREE.Vector3(-26, 30, 0));
127 	
128 	var line13 = new THREE.Line(geometry13, material);
129 	
130 	var geometry14 = new THREE.Geometry();
131     geometry14.vertices.push(new THREE.Vector3(-40, 20.25, 0));
132     geometry14.vertices.push(new THREE.Vector3(-42, 21, 0));
133 	
134 	var line14 = new THREE.Line(geometry14, material);
135 	
136 	var geometry15 = new THREE.Geometry();
137     geometry15.vertices.push(new THREE.Vector3(-40, 19.75, 0));
138     geometry15.vertices.push(new THREE.Vector3(-42, 19, 0));
139 	
140 	var line15 = new THREE.Line(geometry15, material);
141 	
142 	var geometry16 = new THREE.Geometry();
143     geometry16.vertices.push(new THREE.Vector3(-42, 19, 0));
144     geometry16.vertices.push(new THREE.Vector3(-42, 21, 0));
145 	
146 	var line16 = new THREE.Line(geometry16, material);
147 	
148 	var geometry17 = new THREE.Geometry();
149     geometry17.vertices.push(new THREE.Vector3(-42, 21, 0));
150     geometry17.vertices.push(new THREE.Vector3(-43, 22, 0));
151 	
152 	var line17 = new THREE.Line(geometry17, material);
153 	
154 	var geometry18 = new THREE.Geometry();
155     geometry18.vertices.push(new THREE.Vector3(-42, 20, 0));
156     geometry18.vertices.push(new THREE.Vector3(-43, 21, 0));
157 	
158 	var line18 = new THREE.Line(geometry18, material);
159 	
160 	var geometry19 = new THREE.Geometry();
161     geometry19.vertices.push(new THREE.Vector3(-42, 19, 0));
162     geometry19.vertices.push(new THREE.Vector3(-43, 20, 0));
163 	
164 	var line19 = new THREE.Line(geometry19, material);
165 	
166 	scene.add(line);
167  	scene.add(line1);
168 	scene.add(line2);
169 	scene.add(line3);
170 	scene.add(line4);
171 	scene.add(line5);
172 	scene.add(line6);
173 	scene.add(line7);
174 	scene.add(line8);
175 	scene.add(line9);
176 	scene.add(line10);
177 	scene.add(line11);
178 	scene.add(line12);
179 	scene.add(line13);
180 	scene.add(line14);
181 	scene.add(line15);
182 	scene.add(line16);
183 	scene.add(line17);
184 	scene.add(line18);
185 	scene.add(line19);
186 	scene.add(circle);
187 	scene.add(circle1);
188     rr.render(scene, camera);
189 	
190 	var controls = new function()
191 		{
192 			this.jestkost = 0.8;
193 			this.mass = 0.2;
194 			this.g = 0.5;
195 			this.a = 4;
196 			this.l = 16;
197 		}
198 		
199 	var gui = new dat.GUI();
200 	gui.add(controls, 'jestkost', 0.8, Math.PI);
201 	gui.add(controls, 'mass', 0.001, 0.24);
202 	gui.add(controls, 'g', 0.1, 0.98);
203 	
204 	window.addEventListener('resize', onWindowResize, false);
205 	
206 	renderer();
207 		
208 	function onWindowResize()
209 	{
210 		camera.aspect = window.innerWidth/window.innerHeight;
211 		camera.updateProjectionMatrix();
212 		rr.setSize(window.innerWidth, window.innerHeight);
213 		renderer();
214 	}
215 	
216 	function renderer()
217 	{
218 		step+=0.1;
219 		
220 		var koef = controls.mass*controls.g*controls.l*controls.l/(controls.jestkost*controls.a*controls.a);
221 		var arg = Math.sqrt(controls.jestkost*controls.a*controls.a/(controls.mass*controls.l*controls.l));
222 		var koef1 = (line.geometry.vertices[1].y-20)*(line.geometry.vertices[1].y-20);
223 		var koef2 = controls.a/controls.l;
224 		
225 		line.geometry.vertices[1].y=-koef*Math.cos(arg*step)-koef+20;
226 		line.geometry.vertices[1].x=Math.sqrt(controls.l*controls.l-koef1);
227 		line.geometry.verticesNeedUpdate = true;
228 		line1.geometry.vertices[1].y=(-koef*Math.cos(arg*step)-koef+110)*koef2;;
229 		line1.geometry.verticesNeedUpdate = true;
230 		line2.geometry.vertices[1].y=(-koef*Math.cos(arg*step)-koef+80)*koef2;
231 		line2.geometry.vertices[0].y=(-koef*Math.cos(arg*step)-koef+86)*koef2;
232 		line2.geometry.verticesNeedUpdate = true;
233 		line3.geometry.vertices[1].y=(-koef*Math.cos(arg*step)-koef+86)*koef2;
234 		line3.geometry.vertices[0].y=(-koef*Math.cos(arg*step)-koef+90)*koef2;
235 		line3.geometry.verticesNeedUpdate = true;
236 		line4.geometry.vertices[1].y=(-koef*Math.cos(arg*step)-koef+90)*koef2;
237 		line4.geometry.vertices[0].y=(-koef*Math.cos(arg*step)-koef+94)*koef2;
238 		line4.geometry.verticesNeedUpdate = true;
239 		line5.geometry.vertices[1].y=(-koef*Math.cos(arg*step)-koef+94)*koef2;
240 		line5.geometry.vertices[0].y=(-koef*Math.cos(arg*step)-koef+98)*koef2;
241 		line5.geometry.verticesNeedUpdate = true;
242 		line6.geometry.vertices[1].y=(-koef*Math.cos(arg*step)-koef+98)*koef2;
243 		line6.geometry.vertices[0].y=(-koef*Math.cos(arg*step)-koef+102)*koef2;
244 		line6.geometry.verticesNeedUpdate = true;
245 		line7.geometry.vertices[1].y=(-koef*Math.cos(arg*step)-koef+102)*koef2;
246 		line7.geometry.vertices[0].y=(-koef*Math.cos(arg*step)-koef+106)*koef2;
247 		line7.geometry.verticesNeedUpdate = true;
248 		line8.geometry.vertices[1].y=(-koef*Math.cos(arg*step)-koef+106)*koef2;
249 		line8.geometry.vertices[0].y=(-koef*Math.cos(arg*step)-koef+110)*koef2;
250 		line8.geometry.verticesNeedUpdate = true;
251 		circle.position.x=Math.sqrt(controls.l*controls.l-koef1);
252 		circle.position.y=-koef*Math.cos(arg*step)-koef+20;;
253 		circle1.position.x=-40;
254 		circle1.position.y=20; 
255 		requestAnimationFrame(renderer);
256 		rr.render(scene, camera);
257 		
258 		document.getElementById("td1").innerHTML = line.geometry.vertices[1].x;
259 		document.getElementById("td2").innerHTML = line.geometry.vertices[1].y;
260 	}
261 }

Используемые библиотеки

  • gui.js
  • jquery.min.js
  • orbit_controls.js
  • script.js
  • stats.js
  • three.min.js

Возможности программы

  • изменение жесткости пружины
  • изменение ускорения свободного падения

Решение частного случая

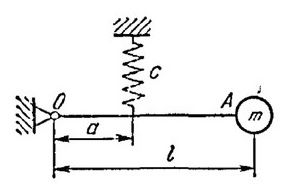
Условия задачи: Стержень [math]OA[/math] длины [math]l[/math], на конце которой помещен груз массы [math]m[/math], может поворачиваться вокруг оси [math]O[/math]. На расстоянии [math]a[/math] от оси [math]O[/math] к стержню прикреплена пружина с коэффициентом жесткости [math]c[/math]. Определить собственную частоту колебаний груза, если стержень [math]OA[/math] в положении равновесия занимает горизонтальное положение. Массой стержня пренебречь.

Решение: [math]y_c[/math] - изменение координаты пружины по y; [math]y[/math] - изменение координаты грузика по y;

[math]T = \frac{m{\dot y}^2}{2}[/math]; [math]y_c = \frac{ya}{l}[/math];

[math]\Pi = -mg + \frac{c}{2}\frac{y^2a^2}{l^2}[/math];

[math] \frac{\partial \Pi}{\partial y} = -mg + \frac{ca^2y}{l^2}[/math];

[math]\frac{d}{dt}\left(\frac{\partial T}{\partial\dot q_i}\right) - \frac{\partial T}{\partial q_i} = \frac{\partial \Pi}{\partial y}[/math];

[math]m\dot v + \frac{ca^2y}{l^2} - mg = 0[/math];

См. также

Источник — «http://tm.spbstu.ru/?title=Колебания_груза_на_пружине&oldid=33947»