КП: Многочастичный симулятор — различия между версиями
| Строка 27: | Строка 27: | ||
Хотим знать, где окажется тело через малое изменение времени - <math>\Delta t</math>. | Хотим знать, где окажется тело через малое изменение времени - <math>\Delta t</math>. | ||
| + | |||
Рассмотрим [[ Интегрирование Верле | базовый метод Верле ]]: | Рассмотрим [[ Интегрирование Верле | базовый метод Верле ]]: | ||
| Строка 42: | Строка 43: | ||
Метод Верле позволяет вычислять траекторию по упрощённой схеме: зная предыдущее и текущее положения (<math>\vec{x}(t - \Delta t)</math> и <math>\vec{x}(t)</math> соответственно) и мгновенное значение равнодействующей приложенных сил в текущем положении <math>\vec{R}(t)</math>. | Метод Верле позволяет вычислять траекторию по упрощённой схеме: зная предыдущее и текущее положения (<math>\vec{x}(t - \Delta t)</math> и <math>\vec{x}(t)</math> соответственно) и мгновенное значение равнодействующей приложенных сил в текущем положении <math>\vec{R}(t)</math>. | ||
| + | |||
| + | Достоинства метода: самокоррекция и бóльшая точность по сравнению с численным методом Эйлера. | ||
Язык реализации: JavaScript. | Язык реализации: JavaScript. | ||
| Строка 47: | Строка 50: | ||
===== Визуализация ===== | ===== Визуализация ===== | ||
Язык рализации: pure SCSS. | Язык рализации: pure SCSS. | ||
| + | |||
Обработка событий: JavaScript. | Обработка событий: JavaScript. | ||
| + | |||
| + | Отказ от WebGL продиктован выбором методов оптимизации для возможности работы с тысячами частиц. | ||
== Решение == | == Решение == | ||
| + | '''[http://cl49743.tmweb.ru/node/phen/pendulum.php Страница решения]''' | ||
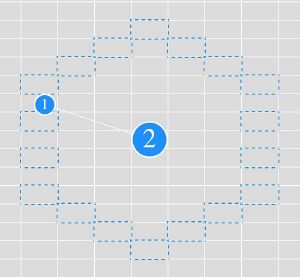
[[File:iPhone_image_2015-4-13-1431495673979_0.jpg|thumb|Нахождение периода в простом движении]] | [[File:iPhone_image_2015-4-13-1431495673979_0.jpg|thumb|Нахождение периода в простом движении]] | ||
===== Элементы системы ===== | ===== Элементы системы ===== | ||
* Частицы; | * Частицы; | ||
| − | * Стержни и пружины<ref>Стержни рассчитываются на расстяжение/сжатие методом коррекции координат. | + | * Стержни и пружины<ref>Стержни рассчитываются на расстяжение/сжатие методом коррекции координат.<br> |
Действие пружин учитывается как действие силы упругости.</ref>; | Действие пружин учитывается как действие силы упругости.</ref>; | ||
* Стенки; | * Стенки; | ||
* Поле сил; | * Поле сил; | ||
* Рабочее окно; | * Рабочее окно; | ||
| + | * Разметка; | ||
* Консоль; | * Консоль; | ||
* Плеер. | * Плеер. | ||
| − | |||
| Строка 75: | Строка 82: | ||
* Воспроизведение/пауза симуляции с заданным <math>\Delta t</math>; | * Воспроизведение/пауза симуляции с заданным <math>\Delta t</math>; | ||
* Скачок вперёд на кратное <math>\Delta t</math> время; | * Скачок вперёд на кратное <math>\Delta t</math> время; | ||
| − | * "Замедление времени". | + | * "Замедление времени".<ref>При малой производительности клиента уменьшаем число отрисовок в единицу времени для сохранения гладкости анимации.</ref> |
== Обсуждение результатов и выводы == | == Обсуждение результатов и выводы == | ||
| Строка 86: | Строка 93: | ||
== Ссылки по теме == | == Ссылки по теме == | ||
Опорный материал: | Опорный материал: | ||
| − | Thomas Jakobsen. "Advanced Character Physics", January 21, 2003. ([http://dkhramov.dp.ua/uploads/Comp/Jakobsen/jakobsen.pdf перевод статьи | + | Thomas Jakobsen. "Advanced Character Physics", January 21, 2003. ([http://dkhramov.dp.ua/uploads/Comp/Jakobsen/jakobsen.pdf перевод статьи <nowiki></nowiki>]) |
== См. также == | == См. также == | ||
Версия 12:27, 13 мая 2015
А.М. Кривцов > Теоретическая механика > Курсовые проекты ТМ 2015 > Многочастичный симуляторКурсовой проект по Теоретической механике
Исполнитель: Старобинский Егор
Группа: 09 (23604)
Семестр: весна 2015
Содержание
Аннотация проекта
Формулировка задачи
Цель работы
Создание интернет-сайта, позволяющего пользователю моделировать многоточечную систему онлайн.
Решаемые задачи
- решение уравнения движения;
- визуализация.
Общие сведения по теме
Уравнение движения
Пусть мы наблюдаем тело в момент времени .
Хотим знать, где окажется тело через малое изменение времени - .
Рассмотрим базовый метод Верле :
, где
- позиция точки,
- равнодействующая всех сил, действующих на тело,
- масса тела,
- текущий момент времени,
- малое изменение времени.
Метод Верле позволяет вычислять траекторию по упрощённой схеме: зная предыдущее и текущее положения ( и соответственно) и мгновенное значение равнодействующей приложенных сил в текущем положении .
Достоинства метода: самокоррекция и бóльшая точность по сравнению с численным методом Эйлера.
Язык реализации: JavaScript.
Визуализация
Язык рализации: pure SCSS.
Обработка событий: JavaScript.
Отказ от WebGL продиктован выбором методов оптимизации для возможности работы с тысячами частиц.
Решение
Элементы системы
- Частицы;
- Стержни и пружины[1];
- Стенки;
- Поле сил;
- Рабочее окно;
- Разметка;
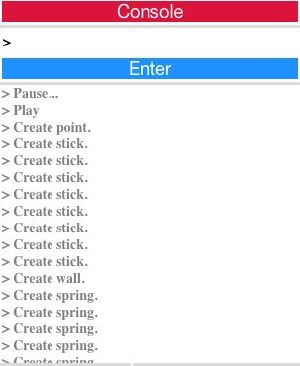
- Консоль;
- Плеер.
Возможности консоли
- Конфигурация начальной системы тел;
- Изменение системы в процессе работы ("на лету");
- Запуск алгоритмов анализа системы;
- Распознавание и вывод ошибок в пользовательских запросах и в исходном коде;
- Распознавани и вывод предупреждений в пользовательских запросах и в исходном коде;
- Тетрис.
Возможности плеера
- Воспроизведение/пауза симуляции с заданным ;
- Скачок вперёд на кратное время;
- "Замедление времени".[2]
Обсуждение результатов и выводы
Скачать отчет:
Скачать презентацию:
Ссылки по теме
Опорный материал: Thomas Jakobsen. "Advanced Character Physics", January 21, 2003. (перевод статьи )