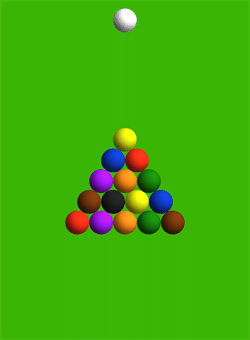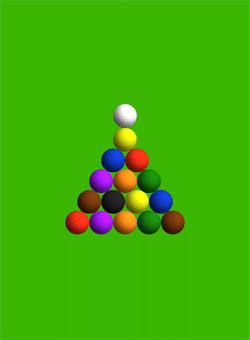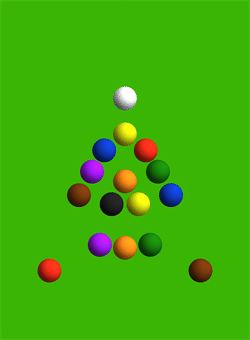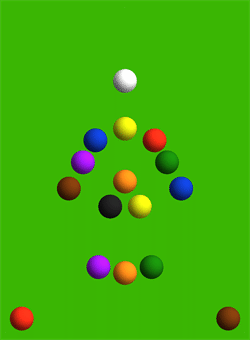КП: Динамика бильярда — различия между версиями
Павел (обсуждение | вклад) (→Общие сведения по теме) |
Павел (обсуждение | вклад) (→Общие сведения по теме) |
||
| Строка 22: | Строка 22: | ||
Прошло более полутораста лет, и математический бильярд развился в свою теорию, породив несколько побочных. «Теория бильярдов» сегодня неотъемлемая часть эргодической теории и теории динамических систем, имеет важнейшее применение в физике. Математиком Гальпериным создан способ определения числа pi с помощью бильярда. Намного ближе общеобразованному читателю результаты исследований математиков Штейнгауза, Альхазена и Гарднера. | Прошло более полутораста лет, и математический бильярд развился в свою теорию, породив несколько побочных. «Теория бильярдов» сегодня неотъемлемая часть эргодической теории и теории динамических систем, имеет важнейшее применение в физике. Математиком Гальпериным создан способ определения числа pi с помощью бильярда. Намного ближе общеобразованному читателю результаты исследований математиков Штейнгауза, Альхазена и Гарднера. | ||
| − | [ | + | File:XM76n.gif |
| + | [[Файл:XM76n.gif|thumb|Стол для русского бильярда|250px]] | ||
== Решение == | == Решение == | ||
Версия 03:11, 6 мая 2015
А.М. Кривцов > Теоретическая механика > Курсовые проекты ТМ 2015 > Динамика бильярда
Курсовой проект по Теоретической механике
Исполнитель: Булдаков Павел
Группа: 09 (23604)
Семестр: весна 2015
Содержание
Аннотация проекта
Формулировка задачи
- Написать программу, моделирующую динамику взаимодействия шаров при игре в Бильярд. Взаимодействие между шарами описывается с помощью потенциала Леннарда-Джонса.
-Рассмотреть классическое разбиение в русском бильярде и подобрать параметры для лучшего начала игры
Общие сведения по теме
Впервые о математическом базисе бильярдной игры заговорил Гаспар Густав Кориолис в своей книге «Théorie mathématique du jeu de billard» (Русск. перевод: «Математическая теория явлений бильярдной игры») в 1835 году. Он использовал в своей работе элементы теории вероятностей, теории пределов и общего анализа. Однако особого интереса у современников (по мнению Лемана) книга не вызвала: ни у математиков, ни у бильярдистов.
Прошло более полутораста лет, и математический бильярд развился в свою теорию, породив несколько побочных. «Теория бильярдов» сегодня неотъемлемая часть эргодической теории и теории динамических систем, имеет важнейшее применение в физике. Математиком Гальпериным создан способ определения числа pi с помощью бильярда. Намного ближе общеобразованному читателю результаты исследований математиков Штейнгауза, Альхазена и Гарднера.
File:XM76n.gif
Решение
Обсуждение результатов и выводы
Скачать отчет:
Скачать презентацию: