Ибраев Д.Ф.: Исследование динамики удара частиц в присутствии жидкой фазы для описания грануляционных процессов — различия между версиями

Версия 17:37, 19 июня 2014

Описание

Данная работа выполнена в рамках Гамбургского проекта при поддержке стипендиальной программы "Леонард Эйлер" немецкой службы академических обменов (DAAD).

Руководители

Руководитель со стороны СПбГПУ: к.ф.-м.н И.Е. Беринский

Руководители со стороны TUHH: Dipl.-Ing. V. Salikov, Prof. Dr.-Ing. S. Antonyuk

Аннотация

Грануляция традиционно считается эмпирическим искусством с большими трудностями в прогнозировании и объяснении наблюдаемых процессов. Промышленность столкнулась с рядом проблем, включая большой процент утилизации, плохой контроль качества продукции, большие расхождения при переходе от лабораторных гранулирующих устройств к промышленным. При условии, что известны соответствующие свойства материала и рабочие параметры, в настоящее время можно сделать полезные предположения о том, как из порошка формируются гранулы.

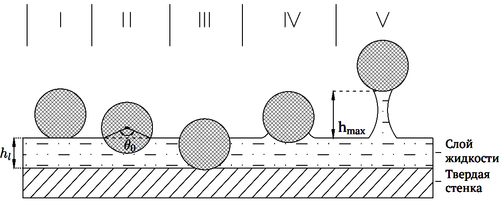
Содержание жидкой фазы при грануляции влияет на свойства столкновений между частицами. Во время этого процесса из-за увлажнения частиц (покрытие частиц жидкой пленкой или каплями) при соударении происходит потеря начальной энергии частиц, которую можно описать с помощью коэффициента восстановления. Реализация соударения двух частиц в лабораторных условиях является технически сложной задачей, поэтому рассматривается удар частицы о смоченную твердую поверхность.

Данная работа состоит из экспериментальной части, аналитического исследования и численного моделирования. В результате серии экспериментов определены коэффициенты восстановления при прямом ударе частиц о твердую поверхность, покрытую тонким слоем жидкости. Рассматривались удары частиц о смоченную поверхность и сухие удары, варьировались скорость частицы до удара и толщина слоя жидкости. Построена аналитическая модель для определения коэффициента восстановления при ударе. Проведено численное моделирование процесса удара с использованием сопряжения ABAQUS и STAR-CCM+. Результаты аналитического и численного моделирования с достаточно высокой точностью совпадают с экспериментальными данными.

Полученные результаты будут использованы при численном моделировании процесса грануляции с последующей разработкой гранулирующего устройства.

Аналитическая модель

В процессе удара частицы о смоченную поверхность на частицы действуют следующие силы: капиллярная сила, сила вязкости, сила сопротивления, сила при контакте частицы со свободной поверхностью жидкости и твердой поверхностью стенки, сила Архимеда и сила тяжести. При моделировании было принято, что влиянием таких сил, как сила вязкости, сопротивления и Архимеда можно пренебречь, исходя из результатов работы [1].

Периоды удара частицы о смоченную твердую поверхность

Закон сохранения энергии для частицы в процессе удара примет вид:

[math] m_0 u_0^2=m_f u_f^2+2L, [/math]

где [math]u_0, u_f[/math] - скорости частиц до удара и после соответственно, [math]m_0[/math] - масса частицы, [math]m_f=\rho_w V_w+m_0[/math] - суммарная масса частицы и жидкости, присоединенной к частице, [math]V_w=\frac{4}{3}\pi(R+h_w)^3-\frac{4}{3}\pi R^3[/math] - объем жидкости на частице после удара, [math]h_w[/math] - толщина слоя жидкости на частице после удара, [math]L[/math] - потеря энергии при ударе.

Коэффициент восстановления частицы при столкновении со стенкой можно записать следующим образом:

[math] e=-\frac{u_f}{u_0}=\sqrt{\frac{m_0}{m_f}-\frac{2L}{m_f u_0^2}} [/math]

Потеря энергии [math]L[/math]:

[math] L = A_{\text{cap}}+L_l+L_{\text{с}}, [/math]

где [math]A_{\text{cap}}[/math] - работа капиллярных сил, [math]L_l[/math] и [math]L_{\text{c}}[/math] - энергия, затраченная на удар частицы о свободную поверхность жидкости и удар о стенку соответственно.

Выражение для капиллярной силы [math]\vec F_{\text{cap}}[/math] было получено в работе [2]. Работа [math]A_{\text{cap}}[/math] выражается следующим образом:

[math] A_{\text{cap}} =\int_0^{h_{max}} \vec{F}_{\text{кап}}d(\vec{e}_{u}D) =\int_0^{h_{max}} 2\pi R \sigma \cos \theta \cdot \left(\displaystyle 1-\frac{1}{\sqrt{1+\frac{2V}{\pi R D^2}}}\right)\vec{e}_n d(\vec{e}_{u}D), [/math]

где [math]D[/math] - расстояние между сферой и стенкой, [math]\sigma[/math] - коэффициент поверхностного натяжения, [math] V = \frac{\pi R}{2} [H^2(b)-D^2][/math] - объем жидкого мостика, [math]b[/math] - радиус смоченной области и [math]H(r)=D+r^2/R[/math].