Корреляции перемещений в кристаллах (компьютерное моделирование) — различия между версиями
Wikiadmin (обсуждение | вклад) |
Wikiadmin (обсуждение | вклад) м |
||
| Строка 10: | Строка 10: | ||
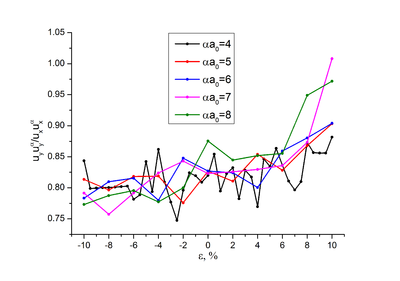
| − | [[Файл:uu_a___3D_Morse_epsion.png|400px|thumb|left|Рис. 1. | + | [[Файл:uu_a___3D_Morse_epsion.png|400px|thumb|left|Рис. 1.3. Зависимость <math>\mathbf{u}\cdot\mathbf{u_\alpha}</math> от <math>{\alpha}{a_0}</math>.]] |
| − | [[Файл:uu_a___3D_Morse_alfa.png|400px|thumb|center|Рис. 1. | + | |
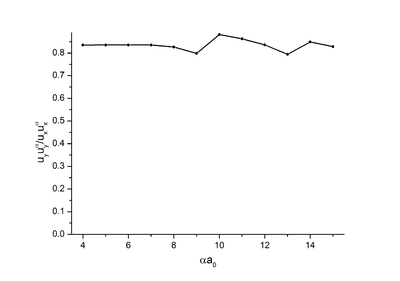
| + | [[Файл:uu_a___3D_Morse_alfa.png|400px|thumb|center|Рис. 1.4. Зависимость <math>\mathbf{u}\cdot\mathbf{u_\alpha}</math> от <math>\epsilon</math>.]] | ||
<br style="clear: both" /> | <br style="clear: both" /> | ||
| Строка 24: | Строка 25: | ||
[[Файл:uu_a___2D_Morse_epsion_alfa.png|400px|thumb|left|Рис. 1.2. Зависимость <math>\mathbf{u}\cdot\mathbf{u_\alpha}</math> от <math>\epsilon</math> при различных <math>{\alpha}{a_0}</math>.]] | [[Файл:uu_a___2D_Morse_epsion_alfa.png|400px|thumb|left|Рис. 1.2. Зависимость <math>\mathbf{u}\cdot\mathbf{u_\alpha}</math> от <math>\epsilon</math> при различных <math>{\alpha}{a_0}</math>.]] | ||
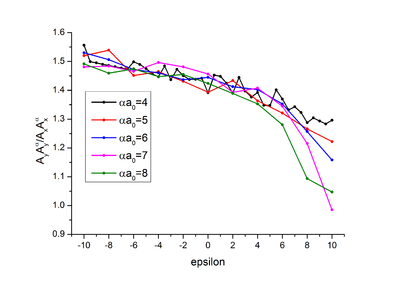
| − | [[Файл:AA_a___2D_Morse_epsion_alfa.png|400px|thumb|center|Рис. 1.1. Зависимость <math>\mathbf{A}\cdot\mathbf{A_\alpha}</math> от <math>\epsilon</math> при различных <math>{\alpha}.]] | + | [[Файл:AA_a___2D_Morse_epsion_alfa.png|400px|thumb|center|Рис. 1.1. Зависимость <math>\mathbf{A}\cdot\mathbf{A_\alpha}</math> от <math>\epsilon</math> при различных <math>{\alpha}{a_0}</math>.]] |
Версия 17:13, 15 марта 2014
Содержание
Корреляция колебаний
ГЦК
Рассчитаны корреляции , , в системе координат связанных со связью и найдено среднее по всем связям. Ось абсцисс направлена по связи, ось ординат перпендикулярно (по другой связи), ось аппликат по векторному произведению абсциссы и ординаты. Тензоры диагональны с точность .
При отсутствии внешних напряжений зависимость от ширины потенциальной ямы для потенциала морзе отсутствует (Рис.1.1).
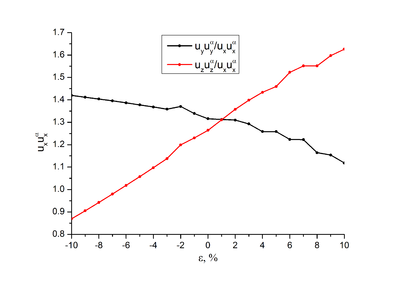
При постоянной ширине потенциальной ямы компоненты зависят от гидростатической деформации линейно, при этом компонента с расширением убывает, а возрастает (Рис.1.2).
2D Треугольная
Рассчитаны корреляции , , в системе координат связанных со связью и найдено среднее по всем связям. Ось абсцисс направлена по связи, ось ординат перпендикулярно (векторное произведение оси абсцисс и вектора перпендикулярного плоскости). Тензоры диагональны с точность .
Отношение перпендикулярной компоненты корреляции к продольной увеличивается при растяжении, и не имеет выраженной зависимости от (Рис.1.3).
Отношение перпендикулярной компоненты корреляции к продольной уменьшается при растяжении, можно заметить слабое уменьшение отношение с ростом (Рис.1.4).
Тепловое расширение
Для определения коэффициента теплового расширения использовалось два подхода: при постоянном объёме и постоянном давлении (с помощью баростата давление приближалось к нулю).
ГЦК
Леннард-Джонс
Постоянный объём
ГЦК кристалл 30x30x30 ГЦК ячеек (??? частиц), периодические граничные условия, релаксация системы в течении 10*Tp, Tp = T0p/200, полное время определения давления 20*Tp, время определения точек среднего 3*Tp. Температура системы от 1e-7*Tk, до 1.9e-6*Tk. На первом шаге задаются начальные скорости согласно нормальному распределению, затем система релаксирует, и далее вычисляется давление на основе метода Кривцова-Кузькина.
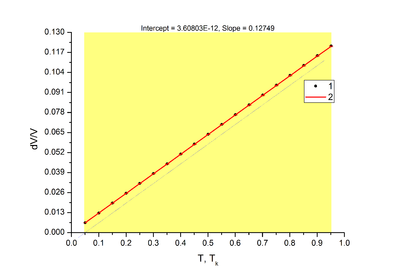
Коэффициент теплового расширения определённый по первой точке: 0.127474, теоретическое значение: 0.131944, относительно отклонение от теоретического значения: 3.39%.
Коэффициент теплового расширения определённый по наклону (Рис.1): 0.12749, теоретическое значение: 0.131944, относительно отклонение от теоретического значения: 3.38%.