Создание модели насыщения связи в простейших углеводородах — различия между версиями

Материал из Department of Theoretical and Applied Mechanics
Перейти к: навигация, поиск
Строка 3: Строка 3:
 
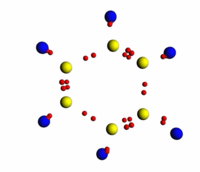
[[Файл:Benz.png|200px|thumb|right]]
 
[[Файл:Benz.png|200px|thumb|right]]
  
−
== Причины создания проекта ==
+
== Аннотация ==
  
−
Общая волновая теория позволяет описывать межатомные взаимодействия, однако имеет ряд недостатков:
+
Метод молекулярной динамики широко используется в различных областях, включая физику, химию, биологию, для того чтобы достичь понимания молекулярных процессов недоступных в эксперименте. Несмотря на то, что наиболее точно описывает межмолекулярные взаимодействия квантовая механика, для практического применения этот метод требует недопустимо много вычислительных ресурсов. С другой стороны Гамильтониан механической системы может быть описан с помощью классических законов механики. В общем случае Гамильтониан состоит из кинетической и потенциальной энергии. Полная кинетическая энергия системы есть сумма всех кинетических энергий частиц. Потенциальная энергия напротив является сложной функцией, описывающей различные взаимодействия между частицами. Вообще говоря функция, описывающая силовое поле, содержит множество параметров, которые должны быть выбраны таким образом, чтобы Гамильтониан точно описывал интересующие нас свойства системы. Параметры системы могут быть выбраны на основании, данных полученных из квантовой механики и экспериментальных данных. Предлагается комбинированный подход основанный на методе молекулярной динамики, эмпирических представлениях квантовой механики и классических законах механики. Целью данного исследования является создание модели, позволяющей проводить компьютерное моделирование атомарных систем, состоящих из большого числа частиц, описывающей насыщение межатомной связи.
  
−
*Общая волновая теория имеет точные решения только для простых систем.
+
==Введение==
−
*Вычислительно слишком сложна
+
В последнее время компьютерное моделирование получило широкое распространение как мощный инструмент для описания физических явлений. Использование потенциалов и описание межатомных взаимодействий с помощью силовых полей получило широкое распространение для моделирования тел с микроструктурой. Подробное описание различных потенциалов и их применения  для описания тел с микроструктурой приведено в работах \cite{Krivtsov_fracture, Alen}. В зависимости от масштаба рассматриваемых явлений могут быть использованы различные компьютерные модели. Для описания систем на электронно ядерном уровне используется теория функционала плотности \cite{DFT}, метод Харти-Фока \cite{Hartee_Fock}. Для моделирования протеинов, липидов и других органических соединений используется силовое поле GROMOS \cite{GROMOS}. Предложенный в 1976 году подход  "QM/MM" в работе \cite{QM_MM}, комбинирующий точность квантово-механического описания и скорость вычислений молекулярной динамики, получил бурное развитие в последнее время и позволил проводить моделирование сложных химических соединений. За работу развитие моделей комплексных химических систем, в основе которой лежит подход "QM/MM", Мартином Карплюсом, Майклом Левиттом и Ари Уоршелом в 2013 была получена Нобелевская премия \cite{Nobel_2013}. Потенциал погруженного атома (embedded atom model, EAM) основанный на теории приближения сильной связи, известной также как модель Финниса-Синклера \cite{finnis}, используется для описания межатомных взаимодейсвий между ионами и окружающего их электронного газа в металлах \cite{eam_potential}. Один из самых простых парных потенциалов, потенциал Леннарда-Джонса \cite{LJ} используется для описания слабых Ван дер Вальсовских взаимодействий сферических неполярных молекул, например в инертных газах. Метод молекулярной динамики стал активно разрабатываться в 50-х годах XX-го столетия Б. Альдером \cite{Alder} и получил широкое развитие. Метод молекулярной динамики позволяет описывать большие атомарные системы (например состоящие из $10^9$ частиц) с помощью решения уравнений динамики Ньютона в 3-х мерном пространстве и позволяет предсказать явления, которые невозможно описать с помощью аналитического подхода или эксперимента. Возможность воспроизведения эксперимента сделало этот метод особенно популярным в последнее время. Исследователь имеет возможность изменять начальные условия и наблюдать влияние этих изменений на конечный результат, что не всегда возможно в условиях реального эксперимента.
−
*Описывает только статическое состояние системы
+
 
 +
Описать систему на электронно-ядерном уровне можно с помощью уравнения Шредингера (\ref{eq:Shrod}) \cite{Dirak}.  
 +
\begin{equation}\label{eq:Shrod}
 +
\hat{H} \Psi = E \Psi,
 +
\end{equation}
 +
\begin{equation} \label{eq:Shrodinger}
 +
\left[T_N + T_e + V_{ee}(r) + V_{NN}(R) + V_{eN}(r,R) \right] \Psi = E \Psi,
 +
\end{equation}
 +
где $T_N$ --- кинетическая энергия ядра, $T_e$ --- кинетическая энергия электронов, $V_{NN}$ --- ядерно-ядерное взаимодействие, $V_{eN}$ --- электронно ядерное взаимодействие и $V_{ee}$ --- электрон-электронное взаимодействие.
 +
\par Волновая функция для системы фермионов может быть записана как функция построенная из одночастичных функций через определитель Слэтера \cite{Slater}:
 +
\begin{align}
 +
\Psi = \frac{1}{\sqrt{N!}}
 +
\begin{vmatrix}
 +
\psi_1( \mathbf{r}_1) & \cdots & \psi_1( \mathbf{r}_N) \\
 +
\vdots& &\vdots \\
 +
\psi_N( \mathbf{r}_1) & \cdots & \psi_N( \mathbf{r}_N) \\
 +
\end{vmatrix}.
 +
\end{align}
  
 
== Представление атома ==
 
== Представление атома ==

Версия 18:40, 18 июня 2015

Проект выполняет Соколов Алексей

Benz.png

Аннотация

Метод молекулярной динамики широко используется в различных областях, включая физику, химию, биологию, для того чтобы достичь понимания молекулярных процессов недоступных в эксперименте. Несмотря на то, что наиболее точно описывает межмолекулярные взаимодействия квантовая механика, для практического применения этот метод требует недопустимо много вычислительных ресурсов. С другой стороны Гамильтониан механической системы может быть описан с помощью классических законов механики. В общем случае Гамильтониан состоит из кинетической и потенциальной энергии. Полная кинетическая энергия системы есть сумма всех кинетических энергий частиц. Потенциальная энергия напротив является сложной функцией, описывающей различные взаимодействия между частицами. Вообще говоря функция, описывающая силовое поле, содержит множество параметров, которые должны быть выбраны таким образом, чтобы Гамильтониан точно описывал интересующие нас свойства системы. Параметры системы могут быть выбраны на основании, данных полученных из квантовой механики и экспериментальных данных. Предлагается комбинированный подход основанный на методе молекулярной динамики, эмпирических представлениях квантовой механики и классических законах механики. Целью данного исследования является создание модели, позволяющей проводить компьютерное моделирование атомарных систем, состоящих из большого числа частиц, описывающей насыщение межатомной связи.

Введение

В последнее время компьютерное моделирование получило широкое распространение как мощный инструмент для описания физических явлений. Использование потенциалов и описание межатомных взаимодействий с помощью силовых полей получило широкое распространение для моделирования тел с микроструктурой. Подробное описание различных потенциалов и их применения для описания тел с микроструктурой приведено в работах \cite{Krivtsov_fracture, Alen}. В зависимости от масштаба рассматриваемых явлений могут быть использованы различные компьютерные модели. Для описания систем на электронно ядерном уровне используется теория функционала плотности \cite{DFT}, метод Харти-Фока \cite{Hartee_Fock}. Для моделирования протеинов, липидов и других органических соединений используется силовое поле GROMOS \cite{GROMOS}. Предложенный в 1976 году подход "QM/MM" в работе \cite{QM_MM}, комбинирующий точность квантово-механического описания и скорость вычислений молекулярной динамики, получил бурное развитие в последнее время и позволил проводить моделирование сложных химических соединений. За работу развитие моделей комплексных химических систем, в основе которой лежит подход "QM/MM", Мартином Карплюсом, Майклом Левиттом и Ари Уоршелом в 2013 была получена Нобелевская премия \cite{Nobel_2013}. Потенциал погруженного атома (embedded atom model, EAM) основанный на теории приближения сильной связи, известной также как модель Финниса-Синклера \cite{finnis}, используется для описания межатомных взаимодейсвий между ионами и окружающего их электронного газа в металлах \cite{eam_potential}. Один из самых простых парных потенциалов, потенциал Леннарда-Джонса \cite{LJ} используется для описания слабых Ван дер Вальсовских взаимодействий сферических неполярных молекул, например в инертных газах. Метод молекулярной динамики стал активно разрабатываться в 50-х годах XX-го столетия Б. Альдером \cite{Alder} и получил широкое развитие. Метод молекулярной динамики позволяет описывать большие атомарные системы (например состоящие из $10^9$ частиц) с помощью решения уравнений динамики Ньютона в 3-х мерном пространстве и позволяет предсказать явления, которые невозможно описать с помощью аналитического подхода или эксперимента. Возможность воспроизведения эксперимента сделало этот метод особенно популярным в последнее время. Исследователь имеет возможность изменять начальные условия и наблюдать влияние этих изменений на конечный результат, что не всегда возможно в условиях реального эксперимента.

Описать систему на электронно-ядерном уровне можно с помощью уравнения Шредингера (\ref{eq:Shrod}) \cite{Dirak}. \begin{equation}\label{eq:Shrod} \hat{H} \Psi = E \Psi, \end{equation} \begin{equation} \label{eq:Shrodinger} \left[T_N + T_e + V_{ee}(r) + V_{NN}(R) + V_{eN}(r,R) \right] \Psi = E \Psi, \end{equation} где $T_N$ --- кинетическая энергия ядра, $T_e$ --- кинетическая энергия электронов, $V_{NN}$ --- ядерно-ядерное взаимодействие, $V_{eN}$ --- электронно ядерное взаимодействие и $V_{ee}$ --- электрон-электронное взаимодействие. \par Волновая функция для системы фермионов может быть записана как функция построенная из одночастичных функций через определитель Слэтера \cite{Slater}: \begin{align} \Psi = \frac{1}{\sqrt{N!}} \begin{vmatrix} \psi_1( \mathbf{r}_1) & \cdots & \psi_1( \mathbf{r}_N) \\ \vdots& &\vdots \\ \psi_N( \mathbf{r}_1) & \cdots & \psi_N( \mathbf{r}_N) \\ \end{vmatrix}. \end{align}

Представление атома

Законы взаимодействия облаков и ядра должны удовлетворять следующим требованиям:

  • Теория отталкивания электронных пар Гиллеспи — Найхолма:
    • «Электронные пары принимают такое расположение на валентной оболочке атома, при котором они максимально удалены друг от друга, т.е. электронные пары ведут себя так, как если бы они взаимно отталкивались»
    • «Все электронные пары, входящие в валентную электронную оболочку, считаются расположенными на одинаковом расстоянии от ядра»

Модель атома

  • Атом состоит из материальных точек, представляющих центры масс ядра и электронных облаков
  • Электронные облака одного атома отталкиваются
  • Ядра разных атомов отталкиваются
  • Электронные облака разных атомов притягиваются
  • Образовавшаяся связь является насыщенной, т.е. взаимодействие электронных облаков, вступивших в связь с облаками других атомом пренебрежимо мало

Результаты

Vin.png Cl.png Meth.png Benz.png

Ссылки

http://www.sciteclibrary.ru/rus/catalog/pages/11938.html

Источник — «http://tm.spbstu.ru/?title=Создание_модели_насыщения_связи_в_простейших_углеводородах&oldid=34842»