Моделирование динамики толпы в областях со сложной геометрией — различия между версиями
Денис (обсуждение | вклад) (→Список использованной литературы) |
Денис (обсуждение | вклад) (→Введение) |
||
| Строка 11: | Строка 11: | ||
Толпа — бесструктурное скопление людей, лишенных ясно осознаваемой общности целей, но взаимно связанных сходством эмоционального состояния и общим объектом внимания. <ref name="def"/> | Толпа — бесструктурное скопление людей, лишенных ясно осознаваемой общности целей, но взаимно связанных сходством эмоционального состояния и общим объектом внимания. <ref name="def"/> | ||
| − | Давка — Скопление теснящихся в беспорядке, давящих друг на друга людей. Давка может привести к получению увечий людьми, поэтому движение должно быть организовано так, чтобы обеспечить умеренное «давление» в толпе. | + | Давка — Скопление теснящихся в беспорядке, давящих друг на друга людей. <ref name="def2"/> Давка может привести к получению увечий людьми, поэтому движение должно быть организовано так, чтобы обеспечить умеренное «давление» в толпе. |
Актуальность данной проблемы подтверждается, например, событиями в 2010 году в Дуйсбурге на фестивале «Love Parade», в ходе которого образовалась давка, в результате которой погиб 21 человек, и было ранено около 500 человек. | Актуальность данной проблемы подтверждается, например, событиями в 2010 году в Дуйсбурге на фестивале «Love Parade», в ходе которого образовалась давка, в результате которой погиб 21 человек, и было ранено около 500 человек. | ||
Версия 14:01, 7 июля 2013
Выполнил: Цветков Д. В.
Научный руководитель: Кривцов А. М.
Презентация: Моделирование динамики толпы
Содержание
Введение
В работе исследуются способы оптимизации движения людей, особенно в условиях паники — ведь в таком случае появляется большой риск получения людьми увечий вследствие увеличения «давления» в толпе.
Толпа — бесструктурное скопление людей, лишенных ясно осознаваемой общности целей, но взаимно связанных сходством эмоционального состояния и общим объектом внимания. [1]
Давка — Скопление теснящихся в беспорядке, давящих друг на друга людей. [2] Давка может привести к получению увечий людьми, поэтому движение должно быть организовано так, чтобы обеспечить умеренное «давление» в толпе.
Актуальность данной проблемы подтверждается, например, событиями в 2010 году в Дуйсбурге на фестивале «Love Parade», в ходе которого образовалась давка, в результате которой погиб 21 человек, и было ранено около 500 человек.
Цель
Цель работы – смоделировать и исследовать движение толпы при различных условиях, найти лучшие способы организации движения в таких местах, как проход в метрополитен, фойе театра, проход в концертный зал, и в других местах, предполагающий переход большого количества людей через некий узкий проём.
Реализация
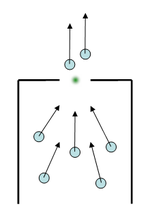
Для моделирования данной задачи используется программа, написанная на языке Java с использованием библиотеки OpenGL. Для описания взаимодействия частиц (людей) используется положительная часть потенциала Леннарда-Джонса – частицы отталкиваются друг от друга, но не притягиваются. Чтобы смоделировать стремление людей попасть в определенную область – на моделирующей области задано векторное поле сил, устремляющее частицу к «выходу»
Для более наглядного отображения результатов моделирования разработаны средства визуализации, позволяющие отобразить достаточное количество частиц и требуемую геометрию области.
Для оценки ситуации измеряются две величины – время прохождения частиц через отверстие, и давление, возникающее в группе частиц. Требуется достичь минимального времени, однако при этом давление не должно превышать некоторого критического значения – чтобы максимально снизить риск травмирования людей в толпе.
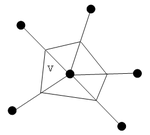
Для расчета давления в системе, используется формула из главы «Техника моделирования» книги А. М. Кривцова «Деформирование и разрушение твердых тел с микроструктурой».
где d – размерность задачи (в нашем случае d = 2),
Fα - воздействие на частицу от окружающих её частиц α,
Aα – расстояние от рассчитываемой частицы до окружающих её частиц,
V – собственное пространство частицы (площадь многоугольника, построенного на половинах расстояний до ближайших частиц)
Для визуализации давлений, действующих на частицу, используется цвет этой частицы – чем больше давление, тем больше смещение к красному концу спектра
Также есть режим демонстрации. В этом режиме вместо сферы используется модель человека, взятая с сайта 3dmodelfree.com. Шаги модели анимированы с использованием системы 3Ds Max, а повороты и скорость шага смоделированы с помощью специально разработанной программной системы визуализации.
Сбор результатов расчетов
После каждого расчета полученные в ходе расчета данные записываются в файл результатов.
Программа может последовательно изменять какие-либо параметры начальной системы – например, можно задать начальное количество частиц – 30, конечное – 60 и шаг – 10. Тогда в автоматическом режиме будут посчитаны системы для 30, 40, 50 и 60 частиц, и после каждого расчета в файл результатов будут добавлены результаты эксперимента (время, затраченное частицами на «выход из комнаты», давления, возникающие в системе.) и его начальные условия. Таким же образом можно изменять и другие параметры – ширину прохода, количество расчетов одной системы, и др.
Для ускорения расчета ресурсоемких систем сделан режим запуска программы без визуализации, также предполагается сделать запись каждого шага в файл, чтобы можно было подробнее рассматривать шаги решения уже рассчитанной системы.
Результаты
I. Время прохождения частиц в зависимости от начального положения.
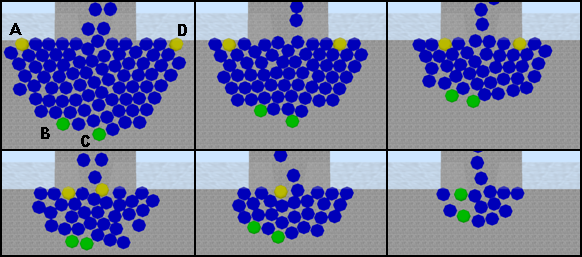
Проведен ряд экспериментов, в ходе которых установлено, что отдельные частицы, находящиеся в точках A и D (см. рисунок), достигают прохода примерно на 25-30% быстрее, чем частицы, находящиеся в точках B и C.
Данные результаты близки к результатам исследований, проведенных В. А. Денисовой в работе «Моделирование социальных процессов», где был проведен и снят на видеокамеру ряд экспериментов у метро «Василеостровская»
II. Время прохождения частиц в зависимости от геометрии прохода.
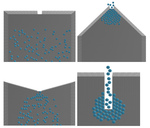
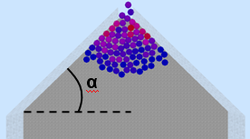
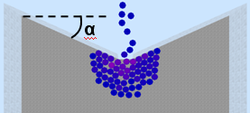
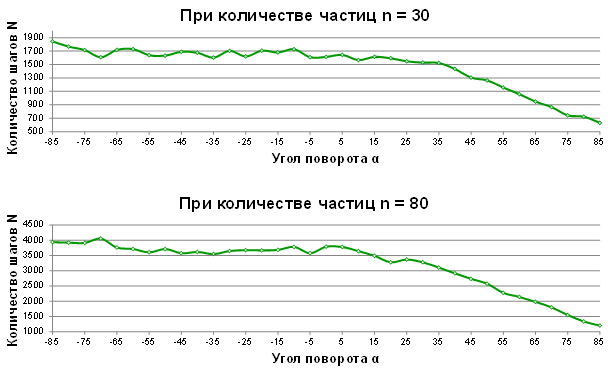
Проведены эксперименты, измеряющие зависимость скорости преодоления частицами прохода в зависимости от геометрии прохода. Единицей измерения времени в данном эксперименте взят шаг интегрирования N. В качестве изменяемой величины геометрии прохода взят угол наклона α стенок у прохода.
Эксперименты проводились в автоматическом режиме с выводом значений в файл. Для каждого угла α проведено 5 экспериментов, и проведено усреднение.
Результаты:
Видно, что при угле поворота от -85° до 15° время преодоления прохода практически одинаково, а при больших углах это время уменьшается с линейной зависимостью. Однако, визуально можно заметить, что при α < 0 давление у входа много меньше, чем при α > 0.
В предельной ситуации (при α = -90°) получаются вертикальные бортики, которые используются у входа некоторых станций метрополитена.
Самое интересное
Здесь можно запустить саму программу в различных конфигурациях и посмотреть, как она работает. Чтобы запустить программу, нужно иметь установленный JRE (JAVA), скачать его можно отсюда [1]
Квадратная геометрия, 60 частиц, модель человека
Расширяющаяся геометрия, 60 частиц, модель шара
Сужающаяся геометрия, 60 частиц, модель шара
Геометрия с бортиками, 40 частиц, модель шара
Геометрия белого зала, 90 частиц, модель человека
Список использованной литературы
- ↑ Психологический лексикон. Энциклопедический словарь в шести томах
- ↑ Ошибка цитирования Неверный тег
<ref>; для сносокdef2не указан текст