Различные методы интегрирования уравнений движения — различия между версиями
(→Вторая задача: результат) |
(→Вторая задача: результат) |
||
| (не показаны 3 промежуточные версии этого же участника) | |||
| Строка 76: | Строка 76: | ||
Метод Верле и Метод Рунге-Кутта с фиксированными границами: | Метод Верле и Метод Рунге-Кутта с фиксированными границами: | ||
| − | [[File:1.png | + | [[File:1.png]] |
| + | |||
| Строка 114: | Строка 115: | ||
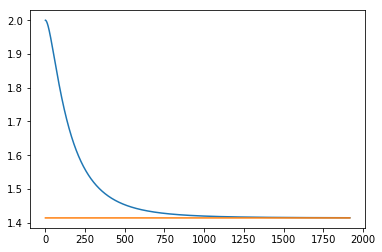
Частица в потенциальной яме Леннарда-Джонса: | Частица в потенциальной яме Леннарда-Джонса: | ||
| − | [[File: | + | [[File:LG.png]] |
Текущая версия на 11:08, 24 января 2020
Курсовой проект по Механике дискретных сред
Исполнитель: Исаева Сабина
Группа: 3630103/60101
Семестр: осень 2019
Содержание
Постановка задачи[править]
1) Сравнить различные методы интегрирования уравнений движения одномерной линейной цепочки (Верле, Рунге-Кутта). Реализовать фиксированные, свободные и периодические граничные условия.
2) Рассмотреть движение частицы в потенциальной яме Леннарда-Джонса: численно определить скорость диссоциации.
Первая задача[править]
Первая задача: решение[править]
Уравнение движения:
Первая задача: метод Верле[править]
Первая задача: метод Рунге-Кутта 4 порядка[править]
Где
Первая задача: граничные условия[править]
Фиксированные граничные условия:
Свободные граничные условия:
Периодические граничные условия:
Первая задача: результат[править]
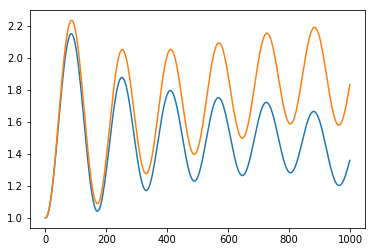
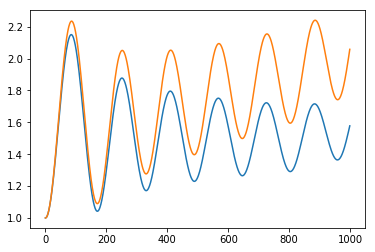
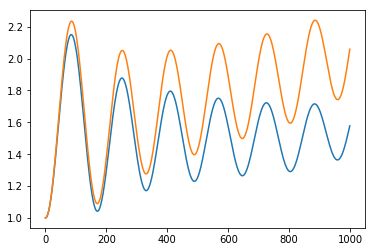
Orange Line- Метод Рунге -Кутта Blue Line-Метод Верле
Метод Верле и Метод Рунге-Кутта с фиксированными границами:
Метод Верле и Рунге -Кутта с периодическими граничными условиями:
Метод Верле и Метод Рунге-Кутта 4 порядка со свободными границами:
Вторая задача[править]
Вторая задача: решение[править]
Уравнение движения частицы в потенциальной яме Леннарда-Джонса:
Где
Вторая задача: дополнительные данные[править]
Начальное положение частицы: